Gratings¶
An optical grating is a periodical structure for the diffraction of light. It can diffract an incoming light beam into several beam travelling in different directions.
1D grating
A 1D grating is periodic in one direction with lattice vector 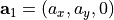 and geometrically invariant in the
and geometrically invariant in the  -direction
(this follows the
-direction
(this follows the JCMsuite convention that the coordinate system for 2D setups is the 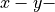 plane),
plane),
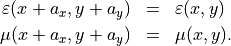
Due to  -invariance the structure appears as lines in 3D:
-invariance the structure appears as lines in 3D:

1D grating.¶
Numerically, the scattering problem reduces to a periodic unit cell of a 2D computational domain, see example Line Grating.
2D grating
A 2D grating is periodic in both horizontal directions. There exist two lattice vectors 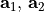 so that the geometry is when shifted by a lattice vector,
so that the geometry is when shifted by a lattice vector,
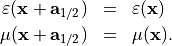
The following figures show a square lattice and a hexagonal lattice arrangement.

Square lattice arrangement. 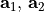 are orthogonal.¶
are orthogonal.¶

Hexagonal lattice arrangement. The lattice vectors 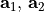 form an angle of
form an angle of 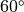 and are of equal length.¶
and are of equal length.¶
For the simulation it is possible to restrict the computation on a unit cell (primitive unit cell), see examples Square Unit Cell and Hexagonal Unit Cell.