Gratings

An optical grating is a periodical structure for the diffraction of light. It can diffract an incoming light beam into several beam travelling in different directions.

1D grating

A 1D grating is periodic in one direction with lattice vector 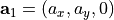\pvec{a}_1 = (a_x, a_y, 0) and geometrically invariant in the z-direction (this follows the JCMsuite convention that the coordinate system for 2D setups is the 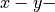x-y- plane),

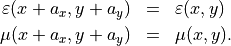
\begin{eqnarray*} \TField{\varepsilon}(x+a_x, y+a_y) & = & \TField{\varepsilon}(x, y) \\ \TField{\mu}(x+a_x, y+a_y) & = & \TField{\mu}(x, y). \end{eqnarray*}

Due to z-invariance the structure appears as lines in 3D:

_images/line_lattice_grating.png

1D grating.

Numerically, the scattering problem reduces to a periodic unit cell of a 2D computational domain, see example Line Grating.

2D grating

A 2D grating is periodic in both horizontal directions. There exist two lattice vectors 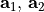\pvec{a}_1,\,\pvec{a}_2 so that the geometry is when shifted by a lattice vector,

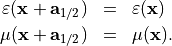
\begin{eqnarray*} \TField{\varepsilon}(\pvec{x}+\pvec{a}_{1/2}) & = & \TField{\varepsilon}(\pvec{x}) \\ \TField{\mu}(\pvec{x}+\pvec{a}_{1/2}) & = & \TField{\mu}(\pvec{x}). \end{eqnarray*}

The following figures show a square lattice and a hexagonal lattice arrangement.

_images/square_lattice_grating.png

Square lattice arrangement. 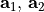\pvec{a}_1,\,\pvec{a}_2 are orthogonal.

_images/hexagonal_lattice_grating.png

Hexagonal lattice arrangement. The lattice vectors 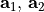\pvec{a}_1,\,\pvec{a}_2 form an angle of 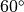60^{\circ} and are of equal length.

For the simulation it is possible to restrict the computation on a unit cell (primitive unit cell), see examples Square Unit Cell and Hexagonal Unit Cell.