Nonlinear Meta Surface (SHG)¶
Second-harmonic generation (SHG) is perhaps the most ubiquitous nonlinear optical process. It involves the generation of optical waves with frequency twice as large as that of an incident pump wave interacting with a nonlinear medium. In this example, we compute the second-harmonic response of a AlGaAs-on-aluminium-oxide monolithic nanodisk embedded in air. The example and parameters are taken from the study by Carletti et al. [1]. The nanodisk is illuminated from above (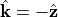
) by a 
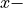polarized, normally incident plane-wave. We analyze SHG process in the undepleted pump approximation, which assumes no back-coupling between the fundamental and SH fields, i.e., the down-conversion process is disregarded. Therefore, we use two-step procedure: in the first step the linear response of the nanodisk at the fundamental (pump) frequency is computed. In the second step, the computed linear electric fields within the domain of interest are used to construct the second-order NonLinearPolarization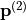 
, which acts as a source term for the second-harmonic signal. Finite-element simulations are then repeated at the SH frequency using this nonlinear source.
The figure below shows the total SH conversion efficiency as a function of the incident fundamental field wavelength. The nanodisk radius and height are fixed at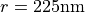 
and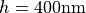 
, respectively. The script data_analysis/run_wavelength_scan.py aims to reproduce the Fig.2 (a) of the considered publication [1].
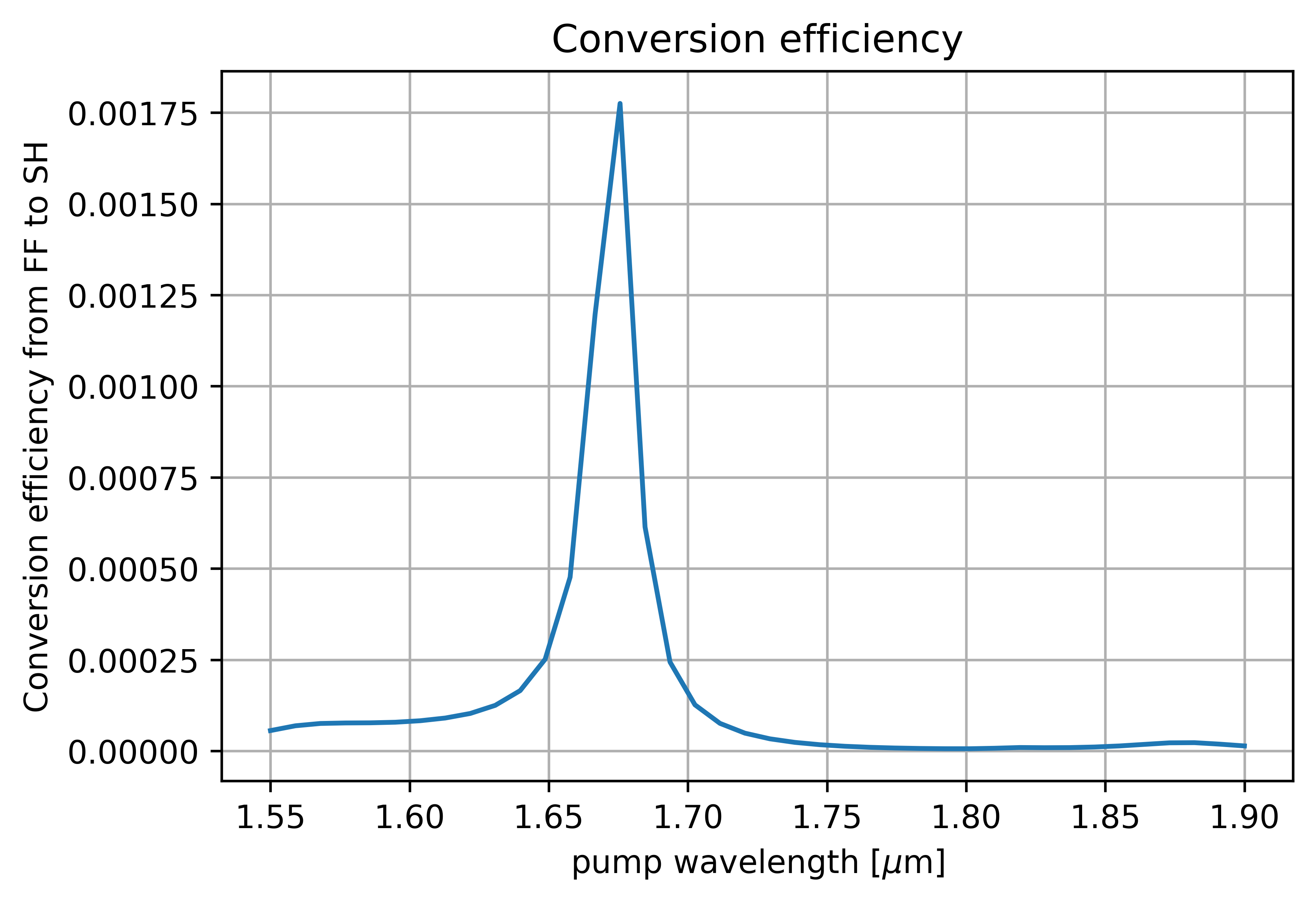
Total SH conversion efficiency as a function of the pump wavelength (, ).¶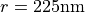
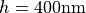Next, we display the SH intensity for the case of an incident wave with fundamental wavelength of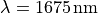 
where the maximum SHG efficiency is obtained. The displayed plot is extracted from the fieldbag generated by SH calculations, and can be reproduced by running the script run_project.py.
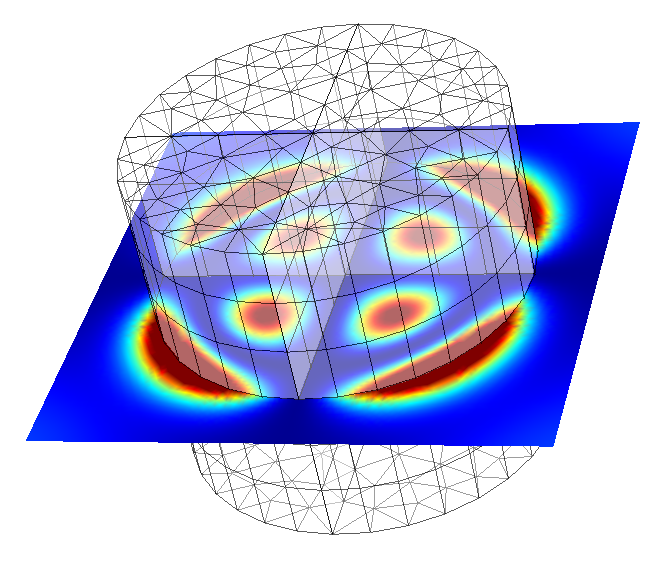
Second-harmonic field intensity on a xz plane crossing through the center of the cylinder.¶
Bibliography
| [1] | (1, 2)
|