Graded Index FiberΒΆ

In this tutorial project the fundamental propagation modes of a graded index fiber are computed. In a graded index fiber, the refractive index of the core is not constant in space but depending on radial distance from the optical axis of the fiber. The functional dependence of refractive index in the core region is defined as a python expression in the file materials.jcm. 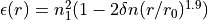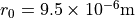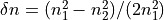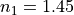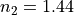In this case the permittivity \epsilon depends on radial distance r as follows: \epsilon(r)=n_1^2(1-2\delta n(r/r_0)^{1.9}) with core radius r_0=9.5\times10^{-6}\mathrm{m}, \delta n=(n_1^2-n_2^2)/(2n_1^2), n_1=1.45, and n_2=1.44.

Compare the syntax in the file materials.jcm:

  • materials.jcm [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
    Material {
  Name = "Cladding"
  DomainId = 1
  RelPermeability = 1.0
  RelPermittivity = 2.0736
}

Material {
  Name = "Core"
  DomainId = 2
  RelPermeability = 1.0
  RelPermittivity {
    Python {
      Expression = "this_radius = power(power(X[0], 2) + power(X[1], 2), 0.5); 
                    delta = (power(n1, 2) - power(n2, 2))/(2*power(n1, 2)); 
                    value = power(n1, 2)*(1 - 2*delta*power((this_radius/radius), exponent_g));
                    value = value*eye(3, 3)"
      Parameter {
        Name = "n1"
        VectorValue = 1.45
      }
      Parameter {
        Name = "n2"
        VectorValue = 1.44
      }
      Parameter {
        Name = "exponent_g"
        VectorValue = 1.9
      }
      Parameter {
        Name = "radius"
        VectorValue = 9.5e-6
      }
    }  
  }
}

Definition of the geometry:

  • layout.jcm [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
    Layout2D {
  UnitOfLength = 1.0e-6
  MeshOptions {
    MaximumSideLength = 15
  }
  Objects {    
    Circle {
      Name = "Cladding"
      DomainId = 1
      Priority = -1
      Radius = 50.0
      RefineAll = 2
      Boundary {
        BoundaryId = 1
        Class = Domain
      }
    }
    Circle {
      Name = "Core"
      DomainId = 2
      Priority = 1
      Radius = 9.5      
      MeshOptions {
        CurvilinearDegree = 2
        MaximumSideLength = 4
      }
    }
  }
}

The tangential electric field components of the fields are expected to be decayed to zero at the boundaries of the computational domain:

  • boundary_conditions.jcm [ASCII]

    1
2
3
4
    BoundaryCondition {
  BoundaryId = 1
  Electromagnetic = TangentialElectric
}

Accuracy settings and post process definitions (here, also the spatially dependent permittivity field is exported for visualization/cross-checking purposes):

  • project.jcmp [ASCII]

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
    Project {
  InfoLevel = 3
  Electromagnetics {
    TimeHarmonic {
      PropagatingMode {
        Lambda0 = 1.55e-06
        FieldComponents = ElectricXYZ
        SelectionCriterion {
          NearGuess {
            Guess = 1.45
            NumberEigenvalues = 2
          }
        }
        Accuracy { 
          FiniteElementDegree = 3
          Precision = 1e-4	  
          Refinement {
            MaxNumberSteps = 1
          }
        }
      }
    }
  }
}

PostProcess {
  ExportFields {
    FieldBagPath = "project_results/fieldbag.jcm"
    OutputFileName = "project_results/permittivity_field.jcm"
    OutputQuantity = RelPermittivity
    Cartesian {
      NGridPointsX = 150
      NGridPointsY = 150
    }
  }
}
PostProcess {
  ExportFields {
    FieldBagPath = "project_results/fieldbag.jcm"
    OutputFileName = "project_results/e_field_cartesian.jcm"
    OutputQuantity = ElectricFieldStrength
    Cartesian {
      NGridPointsX = 150
      NGridPointsY = 150
    }
  }
}

A visualization of the field intensity distribution of a computed mode is shown in the figure below.

_images/graded_index_fiber_intensity.png