Transparent boundaries I¶
Learning targets
- Transparent boundary conditions
- Homogeneous exterior domain
- Non-rectangular computational domain
In many typical models for a simulation, the equations to be simulated are stated for the infinite space (e.g. the light field scattered from a small object is assumed to create a far field which is not bound to a finite domain). In such a case, typically the computational domain is a finite subspace of an infinite space, and so-called transparent boundary conditions are applied to the boundaries of the computational domain. These model the situation that the materials in the exterior domain adjacent to the boundary are continued to infinity.
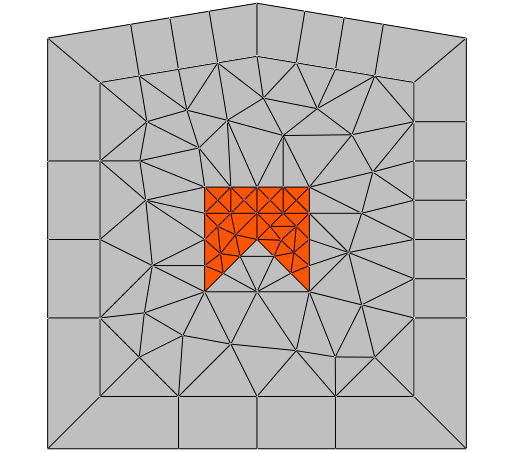
This tutorial example contains a 2D layout with transparent boundaries on all faces of the computational domain. All boundaries of the computational domain touch regions with the same domain identifier. I.e., this geometry models a single object enclosed in an infinite, homogeneous space.
The resulting geometry and mesh correspond to the following figure. Note that the region meshed with triangles corresponds to the computational domain and that the region meshed with quadrilaterals represents the exterior domain which is modeled to extend to infinity.
.jcm Input File
layout.jcm [ASCII]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
Layout2D { Name = "TutorialExample2D" UnitOfLength = 1e-06 MeshOptions { MinimumMeshAngle = 20 MaximumSideLength = 1.5 } Objects { Polygon { Name = "ComputationalDomain/Background" DomainId = 1 Priority = -1 Points = [-3 -3, 3 -3, 3 3, 0 3.5, -3 3] Boundary { Class = Transparent } } Polygon { Name = "Object" DomainId = 2 Priority = 1 Points = [-1 -1, 0 0, 1 -1, 1 1, -1 1] MeshOptions { MaximumSideLength = 0.6 } } } }