Loops¶
In this section we show how to exploit loops (for, while) within Matlab code snippets to define complicated geometries or project setups in a few number of script lines.
Loops within an embedded Matlab code block (cf. previous section Matlab Code Snippets) may extend over several blocks:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | <?
for centerX = [0 : 1 : 9]
keys.center = [centerX 0.0 0.0]
?>
Circle {
Radius = 0.5
GlobalPosition = %(center)e
...
}
<?
end
?>
|
Here, a for-loop starts in line 2 within the first Matlab block. This loop is closed in line 13 after a .jcm code block (lines 6-10). Line 3 dynamically sets the value for key center, which serves as circle’s center in line 8. This way, we have defined ten circles, equally spaced in 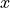 -direction.
-direction.
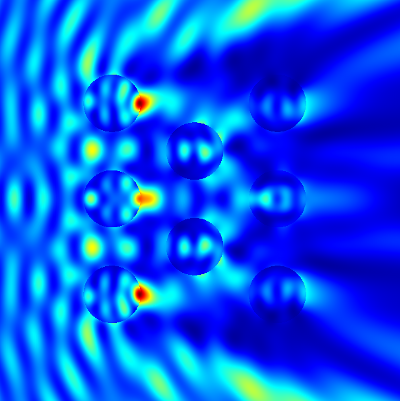
To see how this works in practice, we want to compute the light scattering off multiple rods aligned on a hexagonal lattice. Figure “Multiple rod geometry” shows the setup.
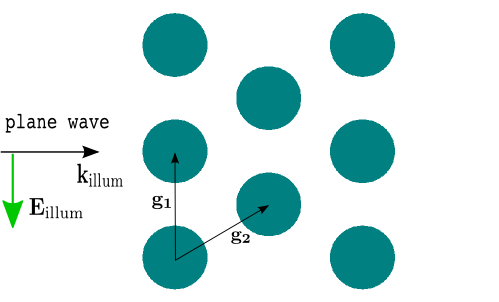
Multiple rod geometry¶
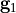 and
and 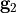 are called grid vectors. For a hexagonal alignment we have
are called grid vectors. For a hexagonal alignment we have
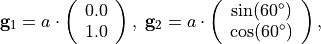
with a lattice parameter  , which is passed as a further parameter in the driver script:
, which is passed as a further parameter in the driver script:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | %% set problem parameter
keys.radius = 0.3;
keys.n_air = 1.0;
keys.n_glass = 1.52;
keys.lambda_0 = 0.550; % in um
keys.polarization = 45; % in degree
keys.a = 1.0;
keys.n_rods = [3 3];
%% run the project
results = jcmwave_solve('mie2D.jcmp', keys);
%% get scattering cross section
scattering_cross_section = ...
results{2}.ElectromagneticFieldEnergyFlux{1};
fprintf('\nscattering cross section: %.8g\n', ...
real(scattering_cross_section));
%% plot exported cartesian grid within matlab:
cfb = results{3};
amplitude = cfb.field{1};
intensity = sum(conj(amplitude).*amplitude, 3);
pcolor(cfb.X, cfb.Y, intensity);
shading interp; view(0, 90); axis equal;
|
In line 8 we set the number of rods in 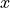 - and
- and 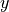 - direction. Figure “Intensity” shows the computed intensity of the electric field.
- direction. Figure “Intensity” shows the computed intensity of the electric field.
For this problem you again find a driver run_geo.m which only runs the mesh generation:
%% set geometry parameters
keys.radius = 0.3;
keys.a = 1.0;
keys.n_rods = [3 3];
%% generate mesh file only
jcmwave_geo('.', keys);
%% open grid.jcm in JCMview
jcmwave_view('grid.jcm');
You can use this script to “play” with the geometry parameters and to watch how the geometry is updated.
In the following we want to discuss the updated layout file:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | <?
% compute grid vectors for hexagonal grid
gv1 = [0.0 keys.a];
gv2 = [sind(60) cosd(60)]*keys.a;
% compute computational domain enclosing all scatterer
maxX = (keys.n_rods(1)-1)*gv2(1);
maxY = (keys.n_rods(2)-1)*gv1(2);
keys.computational_domain_X = maxX+2*keys.radius+2;
keys.computational_domain_Y = maxY+2*keys.radius+2;
?>
Layout {
UnitOfLength = 1e-6
MeshOptions {
MaximumSidelength = 0.1
}
# Computational domain
Parallelogram {
DomainId = 1
Width = %(computational_domain_X)e
Height = %(computational_domain_Y)e
# set transparent boundary conditions
BoundarySegment {
BoundaryClass = Transparent
}
}
<?
center_array = [maxX/2 maxY/2];
for iX=0 : keys.n_rods(1)-1
col_start = [iX*gv2(1) mod(iX, 2)*gv2(2)];
for iY=0 : keys.n_rods(2)-1-mod(iX, 2);
keys.center = col_start+iY*gv1-center_array;
?>
# Scatterer (rod)
Circle {
DomainId = 2
Radius = %(radius)e
GlobalPosition = %(center)e
RefineAll = 4
}
<?
end
end
?>
}
|
The first Matlab block computes the grid vectors 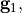
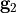 (lines 2-4), and adapts the computational domain size to enclose all rods (lines 6-11). There,
(lines 2-4), and adapts the computational domain size to enclose all rods (lines 6-11). There, maxX and maxY are the dimensions of the array of rods in 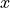 and
and 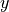 .
.
The Matlab block from lines 34-42 defines two for loops over the number of rods in 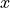 and
and 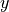 . Line 39 sets the center of the current rod, which is used in line 46 in the enclosed
. Line 39 sets the center of the current rod, which is used in line 46 in the enclosed .jcm block (center_array is used to shift the center of the array of rods to the origin). The for loops are closed in the last Matlab block (lines 51-54).