Rotation¶
| Type: | Rotation |
|---|---|
| Range: | [SO(3)] |
| Default: | -/- |
| Appearance: | optional |
The Rotation parameter defines a coordinate transformation applied to the NonLinearSusceptibility tensor.
We define the rotation matrix 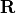 which transforms the laboratory frame (the internal coordinate system of the linear JCM-fieldbag) to the crystal’s principal axis system (crystalline coordinates). For example of second-order nonlinear process, the
which transforms the laboratory frame (the internal coordinate system of the linear JCM-fieldbag) to the crystal’s principal axis system (crystalline coordinates). For example of second-order nonlinear process, the NonLinearPolarization in laboratory frame is defined as:

where

is the NonLinearPolarization in crystalline coordinates, and 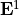 and
and 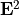 are the computed linear fields.
are the computed linear fields.