ModeOverlap¶

Type:	section
Appearance:	simple
Excludes:	CartesianToFourierTransform, ConvertToPowerFlux, CreateReducedBasis, DensityIntegration, DipoleEmission, EvaluateReducedBasis, ExportFields, ExportGrid, FarField, FluxIntegration, FourierTransform, GridStatistics, IntegrationWeights, LayeredMediaSolver, MultipoleExpansion, OpticalImaging, PupilField, Radiation, ResonanceExpansion, ResonanceOverlap, ScatteringMatrix, Superposition, SurfaceDensityIntegration

This post process computes the overlap of scattered electromagnetic field with the modes obtained from a waveguide simulation. This information is for example of interested when computing the coupling efficiency of a light source into a waveguide or glass fiber, or in simulations of integrated photonic circuits, when transition behavior of multi port devices like split ring resonators, y-splitters or curved waveguides are analyzed.

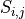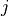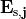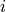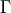The overlap $S_{i,j}$ of the $j$ -th scattered field $\VField{E_{\mathrm{s},j}}$ with the $i$ -the waveguide mode $\VField{E_{\mathrm{m},i}}$ on a plane port $\Gamma$ is defined by:

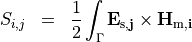
$\begin{eqnarray*} S_{i, j} & = & \frac{1}{2} \int_{\Gamma} \VField{E_{\mathrm{s},j}} \times \VField{H_{\mathrm{m}, i}} \end{eqnarray*}$

where 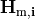$\VField{H_{\mathrm{m}, i}}$ is the corresponding magnetic field of the mode.

Note

The mode fields (as a result of a propagating mode problem) are orthonormal with respect to the above scalar product, that is

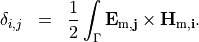
$\begin{eqnarray*} \delta_{i, j} & = & \frac{1}{2} \int_{\Gamma} \VField{E_{\mathrm{m},j}} \times \VField{H_{\mathrm{m}, i}}. \end{eqnarray*}$

Therefore, the mode-wise incoupled power flux is given by

$\begin{eqnarray*} P_{i, j} & = & |S_{i, j}|^2. \end{eqnarray*}$

You can explicitly specify the port 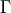$\Gamma$ within the section Port. Otherwise, the boundary of the computational domain is automatically matched with the geometry of the waveguide simulation to find all matching ports 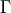$\Gamma$ where the overlap is computed. The header of the created table file contains the positions and outer normals of the found ports.

Note

The above semi-scalar product uses the holomorphic form of the Poynting vector. Up to a phase shift, the resulting coupling coefficients are the same for loss-free, non-active materials as when using a Poynting vector based scalar product (conjugate the magnetic field). The above mentioned mode-orthonormality is only true for damped materials or leaky modes, when using the holomorphic form.