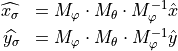PlaneWave¶

Type:	section
Appearance:	multiple

Specifies a time-harmonic plane wave,

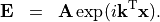
$\begin{eqnarray*} \VField{\VField{E}} & = & \VField{A} \exp(i \tvec{k}^{\mathrm{T}} \pvec{x}). \end{eqnarray*}$

There are three ways for a user input of a plane wave:

Specify all components of $\tvec{k}$ and $\VField{A}$ , see here.
Specify incidence angles 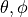$\theta, \phi$ and polarization in terms of 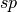$sp$ -components, see here.
Specify pupil 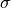$\sigma$ -coordinates and polarization in terms of 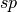$sp$ -components or 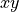$xy$ -components, see here.

The following figure show the situation for a incident plane wave from below and from top.

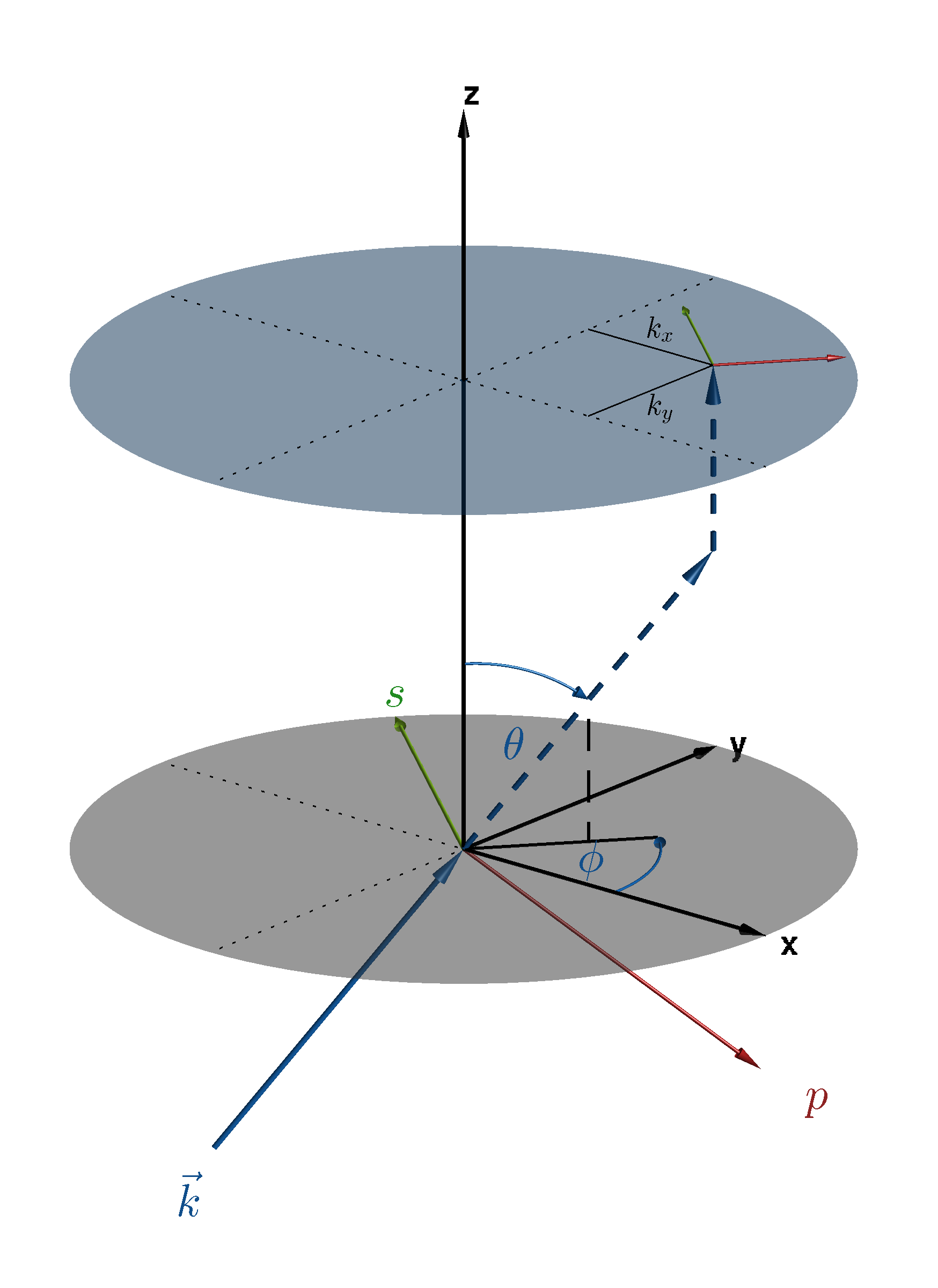
Plane Wave from below. The upper light blue plane is the $\sigma$ -plane.¶

Plane wave from above. The upper light blue plane is the $\sigma$ -plane.¶

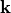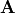
Definition by $\tvec{k}$ and $\VField{A}$

In order to be a solution of Maxwell’s equations in an homogeneous medium it is required that the wave vector 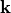$\tvec{k}$ and the complex-valued field amplitude 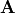$\VField{A}$ are perpendicular, e.g., 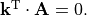$\tvec{k}^{\mathrm{T}}\cdot \VField{A} = 0.$ The wave vector, 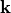$\tvec{k}$ , is related to the vacuum wavelength, 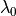$\lambda_0$ , of the plane wave and to the refractive index, 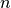$n$ , of the medium from where the plane wave is coming in by $|\tvec{k}|=2\pi n/\lambda_0$ .

When globally defined, e.g, when DomainId and BoundaryId are left empty, this field is interpreted as an incident plane wave light source. Then, the wavevector 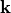$\tvec{k}$ is specified in the medium from where the plane wave is coming in. When the exterior domain of the corresponding geometry is layered, then Maxwell’s equations are first automatically solved for the unstructured layered media stack under the given plane illumination, and the corresponding solution is applied as source field. .. a field is specified which solves Maxwell’s equation within the layered media stack under the given illumination.

Amplitude (polarization and phase) and K (propagation direction and wavelength) deliver a unique description of plane waves. For convenience, JCMwave provides some more options to define a plane wave:

Definition by 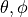$\theta, \phi$

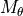ThetaPhi defines the propagation direction. With the rotation matrices $M_{\varphi}$ and $M_{\theta}$ and the unit vector 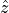$\hat{z}$ the wave vector 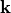$\tvec{k}$ is calculated as follows:

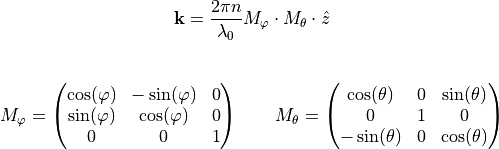
$\begin{eqnarray*} \tvec{k} = \frac{2 \pi n}{\lambda_0} M_{\varphi} \cdot M_{\theta} \cdot \hat{z} \end{eqnarray*} \begin{eqnarray*} M_{\varphi} = \begin{pmatrix} \cos(\varphi) & -\sin(\varphi) & 0 \\ \sin(\varphi) & \cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} \qquad M_{\theta} = \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} \end{eqnarray*}$

With the Parameter Incidence one specifies if $\hat{z}$ points in direction of $z$ (FromBelow) or $-z$ (FromAbove). The refractive index 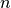$n$ is the refractive index of the lower half space (Incidence=FromBelow) or the upper half space (Incidence=FromAbove). We further need to define vacuum wavelength Lambda0 or alternatively the angular frequency Omega, that is

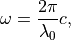
$\begin{eqnarray*} \omega = \frac{2\pi}{\lambda_0} c, \end{eqnarray*}$

with $c$ being the speed of light in vacuum. We use the 2-vector parameter SP, $[\VField{\VField{E}}_s, \VField{\VField{E}}_p]$ to specify the polarization of the plane wave:

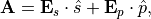
$\begin{eqnarray*} \VField{A} = \VField{\VField{E}}_s \cdot \hat{s}+\VField{\VField{E}}_p \cdot \hat{p}, \end{eqnarray*}$

with

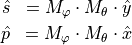
$\begin{eqnarray*} \hat{s} & = M_{\varphi} \cdot M_{\theta} \cdot \hat{y} \\ \hat{p} & = M_{\varphi} \cdot M_{\theta} \cdot \hat{x} \end{eqnarray*}$

Definition by 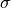$\sigma$ -coordinates

Another option to provide the propagation direction is Sigma,

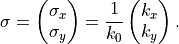
$\begin{eqnarray*} \tvec{\sigma} = \begin{pmatrix} \sigma_x \\ \sigma_y \\ \end{pmatrix} = \frac{1}{k_0} \begin{pmatrix} k_x \\ k_y \\ \end{pmatrix}. \end{eqnarray*}$

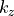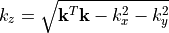The $k_z$ component of of the incident plane wave is computed from the relation $k_z = \sqrt{\tvec{k}^T\tvec{k}-k_x^2-k_y^2}$ .

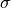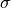Ray optically the $\sigma$ plane shown in the above figures can be regarded as the pupil plane of an optical system with optical axis in $+z$ -direction imaging the incident plane wave towards infinity. The so mapped incident plane wave is perpendicular to the $\sigma$ -plane and the field vector lies within the 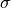$\sigma$ -plane.

Instead of specifying the 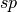$sp$ -components of the polarization one alternatively can define the polarization in the Cartesian coordinates of the 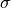$\sigma$ pupil plane:

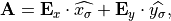
$\begin{eqnarray*} \VField{A} = \VField{\VField{E}}_x \cdot \widehat{x_\sigma}+\VField{\VField{E}}_y \cdot \widehat{y_\sigma}, \end{eqnarray*}$

with

$\begin{eqnarray*} \widehat{x_\sigma} & = M_{\varphi} \cdot M_{\theta} \cdot M_{\varphi}^{-1}\hat{x} \\ \widehat{y_\sigma} & = M_{\varphi} \cdot M_{\theta} \cdot M_{\varphi}^{-1} \hat{y} \end{eqnarray*}$