DifferentialEvolutionOptimization¶

Purpose¶

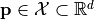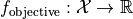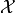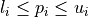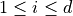The purpose of the driver is to identify a parameter vector $\mathbf{p}\in\mathcal{X}\subset\mathbb{R}^d$ that minimizes the value of an objective function $f_\text{objective}: \mathcal{X} \rightarrow \mathbb{R}$ . The search domain $\mathcal{X}$ is bounded by box constraints $l_i\leq p_i \leq u_i$ for $1\leq i\leq d$ and may be subject to several constraints 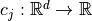$c_j: \mathbb{R}^d \rightarrow \mathbb{R}$ such that 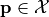$\mathbf{p} \in \mathcal{X}$ only if 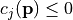$c_j(\mathbf{p}) \leq 0$ (see create_study()).

The driver uses the heuristic evolutionary approach to search globally for a minimum of the objective function. We recommend to use Bayesian optimization to search globally for a minimum. Only if the evaluation times of the objective function are very short (smaller than 1-3 seconds) it can be beneficial to use differential evolution.

The implementation of the driver is based on the open source implementation of scipy (see https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html).

Usage Example¶

import sys,os
import numpy as np
import time

sys.path.append(os.path.join(os.getenv('JCMROOT'), 'ThirdPartySupport', 'Python'))
import jcmwave
client = jcmwave.optimizer.client()


# Definition of the search domain
domain = [
    {'name': 'x1', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'x2', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'radius', 'type': 'fixed', 'domain': 2},
]

# Definition of a constraint on the search domain
constraints = [
    {'name': 'circle', 'constraint': 'sqrt(x1^2 + x2^2) - radius'}
]

# Creation of the study object with study_id 'DifferentialEvolutionOptimization_example'
study = client.create_study(domain=domain, constraints=constraints,
                            driver="DifferentialEvolutionOptimization",
                            name="DifferentialEvolutionOptimization example",
                            study_id='DifferentialEvolutionOptimization_example')

# Definition of a simple analytic objective function.
# Typically, the objective value is derived from a FEM simulation
# using jcmwave.solve(...)
def objective(**kwargs):
    time.sleep(2) # makes objective expensive
    observation = study.new_observation()
    x1,x2 = kwargs['x1'], kwargs['x2']
    observation.add(10*2
                + (x1**2-10*np.cos(2*np.pi*x1))
                + (x2**2-10*np.cos(2*np.pi*x2))
            )

    return observation

# Set study parameters
study.set_parameters(max_iter=80, num_parallel=2)

# Run the minimization
study.set_objective(objective)
study.run()

info = study.info()
print('Minimum value {:.3f} found for:'.format(info['min_objective']))
for param,value in info['min_params'].items():
    if param == 'x4': print('   {}={}'.format(param,value))
    else: print('   {}={:.3f}'.format(param,value))

Parameters¶

The following parameters can be set by calling, e.g.

study.set_parameters(example_parameter1 = [1,2,3], example_parameter2 = True)

max_iter (int):	Maximum number of evaluations of the objective function (default: inf)

max_time (int):	Maximum run time in seconds (default: inf)

num_parallel (int):
	Number of parallel observations of the objective function (default: 1)

eps (float):	Stopping criterium. Minimum distance in the parameter space to the currently known minimum (default: 0.0)

min_val (float):
	Stopping criterium. Minimum value of the objective function (default: -inf)

num_initial (int):
	Number of independent initial optimizers (default: 1)

max_num_minimizers (int):
	If a minimizer has converged, it is restarted at another position. If max_num_minimizers threads have converged, the optimization is stopped (default: inf)

sobol_sequence (bool):
	If true, all initial samples are taken from a Sobol sequence. This typically improves the coverage of the parameter space. (default: True)

popsize_multiplier (int):
	A multiplier for setting the total population size. The population has popsize * len(x) individuals. (default: 15)

tol (float):	The optimizer stops when the mean of the population energies (objective function values), multiplied by tol is larger than the standard deviation of the population energies. (default: 0.0)

strategy (str):	The differential evolution strategy to use. (default: best1bin) (options: [‘best1bin’, ‘best1exp’, ‘rand1exp’, ‘randtobest1exp’, ‘best2exp’, ‘rand2exp’, ‘randtobest1bin’, ‘best2bin’, ‘rand2bin’, ‘rand1bin’])

mutation (float or tuple (min,max)):

Controls the mutation constant also known as differential weight, being denoted by F.If specified as a float it should be in the range [0, 2]. If specified as a tuple (min, max) dithering is employed. Dithering randomly changes the mutation constant on a generation by generation basis. The mutation constant for that generation is taken from U[min, max). Dithering can help speed convergence significantly. Increasing the mutation constant increases the search radius, but will slow down convergence. (default: (0.5, 1))

recombination (float):
	The recombination constant, should be in the range [0, 1]. In the literature this is also known as the crossover probability, being denoted by CR. Increasing this value allows a larger number of mutants to progress into the next generation, but at the risk of population stability. (default: 0.7)