Parameter Reconstruction¶
In this tutorial we briefly discuss how we can perform a parameter reconstruction using a Mueller matrix ellipsometry dataset. We use the same project files that were also used in the discussion on Mueller matrix ellipsometry in the EM tutorial example.
We assume that we have acquired a set of measurements from a Mueller matrix ellipsometry
experiment on a grating, that was performed for a series of different incident light
wavelengths 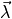 . These measurements are arranged in a target vector
. These measurements are arranged in a target vector
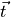 . As we control its construction we know which Mueller matrix element and wavelength contributes to which vector element.
We further assume that we can assign a measurement uncertainty
to each of the components in
. As we control its construction we know which Mueller matrix element and wavelength contributes to which vector element.
We further assume that we can assign a measurement uncertainty
to each of the components in 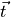 , we denote the measurement uncertainty vector
as
, we denote the measurement uncertainty vector
as 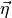 . Please note that the actual ordering of the components within the
vector is of no importance for the reconstruction.
. Please note that the actual ordering of the components within the
vector is of no importance for the reconstruction.
The information contained in the target vector 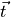 can be used to infer the
geometrical parameters of the investigated grating. This can be done by solving an inverse
problem. The approach for this is as follows. A parameterized model of the measurement
process is created. The model parameters are then varied in a systematic fashion, until a
set of model parameters is determined for which the calculated output of the model is
similar to the set of experimental measurements of the grating.
can be used to infer the
geometrical parameters of the investigated grating. This can be done by solving an inverse
problem. The approach for this is as follows. A parameterized model of the measurement
process is created. The model parameters are then varied in a systematic fashion, until a
set of model parameters is determined for which the calculated output of the model is
similar to the set of experimental measurements of the grating.
The parameterized model for the Mueller matrix ellipsometry experiment is created using
JCMsuite. A function is created which computes the Mueller matrix entries  using the FEM model for the same set of incident wavelengths
using the FEM model for the same set of incident wavelengths 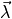 that
were used during the actual experiment. This involves the Fourier transformation and the
scattering matrix postprocesses discussed in the EM tutorial. The various matrix entries
are assembled in a vector
that
were used during the actual experiment. This involves the Fourier transformation and the
scattering matrix postprocesses discussed in the EM tutorial. The various matrix entries
are assembled in a vector  with the same ordering as the target vector
with the same ordering as the target vector
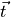 , and then returned.
, and then returned.
The actual parameter reconstruction, that is the fit of the model output to the target
vector, can efficiently be performed using the BayesLeastSquare driver of the analysis and
optimization toolbox within the Driver Reference. The approach is closely related to Bayesian
optimization and similarly employs Gaussian processes (a machine learning surrogate
model), and allows to perform a global black box optimization of the least-squares
problems. By using Gaussian processes the method is very well suited for expensive model
functions, such as a wavelength dependent Mueller matrix calculation and is capable of
finding a set of model parameters that explain the experiment in fewer iterations than
conventional methods. An in-depth discussion and explanation of the approach is presented
in an article on
our Blog.
The optimization script is set up in a very similar fashion as the one in the Optimization tutorial. An archive to perform the reconstruction locally can be downloaded here. The complete script looks as follows. Please note that some logic is abstracted away into imported files.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 | """Parameter reconstruction using JCMsuite
The details of the employed reconstruction are described in [1].
[1] https://onlinelibrary.wiley.com/doi/10.1002/adts.202200112
"""
import pathlib
import pandas as pd
import jcmwave
import numpy as np
from matplotlib import pyplot as plt
from utils.forward_problem import ForwardProblem
# from utils.generate_test_data import generate_test_data
from utils.material import SiMaterial
##############################################################################
# Parameters to play with
# Number of parallel jobs in JCMsolve; for demo version only 1 is allowed
MULTIPLICITY: int = 1
# Using derivatives of the FEM model for the reconstruction; speeds up the reconstruction
DERIVATIVE_ORDER: int = 1
# FEM degree of the JCMsuite model
FEM_DEGREE: int = 3
# Number of iterations in the optimization
NUM_ITERATIONS: int = 20
##############################################################################
# Register the localhost as a machine to perform computations
jcmwave.daemon.add_workstation(
Hostname="localhost",
#
# Number of parallel jobs
Multiplicity=MULTIPLICITY,
#
# Each parallel job runs with this number of threads. Use at least 2.
NThreads=2,
)
def main():
# Path to JCM project
root_dir = pathlib.Path(__file__).parent
data_dir = root_dir / "data"
jcm_project_dir = root_dir / "jcm"
project_file = jcm_project_dir / "project.jcmpt"
optimization_dir = pathlib.Path(__file__).parent
optimization_dir_str = str(optimization_dir.absolute())
study_id = "Ellipsometry_reconstruction_example"
# Remove any previous results
(optimization_dir / f"{study_id}.jcmo").unlink(missing_ok=True)
target_keys = pd.read_csv(data_dir / "target_parameters.csv")
target_keys = pd.Series(
target_keys.Value.values, index=target_keys.Parameter
).to_dict()
target_values = pd.read_csv(data_dir / "target_values.csv")
target_vector = target_values["target_vector"].to_numpy()
uncertainty_vector = target_values["uncertainty_vector"].to_numpy()
# Model parameters
model_param_keys = dict(
# Varying geometry
h=55,
width=31,
swa=88,
radius=8,
)
# Rest of the parameters for the JCMsuite project
keys = dict(
# Numerical parameters
derivative_order=DERIVATIVE_ORDER,
fem_degree=FEM_DEGREE,
precision=1e-3,
# Material parameters; n3 is overridden by the material file
n1=1,
n2=1.4,
n3=1.967 + 4.443 * 1j,
# Illumination
theta=65,
phi=45,
vacuum_wavelength=365e-9,
)
# Merge the two
keys.update(model_param_keys)
wavelengths = np.linspace(266, 800, 11)
fem_problem = ForwardProblem(project_file, wavelengths, SiMaterial())
# Four dimensions
optimization_domain = [
{"name": "h", "type": "continuous", "domain": [50, 60]},
{"name": "width", "type": "continuous", "domain": [25, 35]},
{"name": "swa", "type": "continuous", "domain": [84, 90]},
{"name": "radius", "type": "continuous", "domain": [6, 8]},
]
print()
print("The target parameter to be reconstructed is")
for parameter in optimization_domain:
print(f"\t{parameter['name']}: {target_keys[parameter['name']]}")
print()
print(
"Derivative information of the FEM solver is {}".format(
"being used" if keys["derivative_order"] > 0 else "not being used"
)
)
print()
client = jcmwave.optimizer.client()
# Creation of the study object with study_id 'BayesLeastSquare_example'
study = client.create_study(
domain=optimization_domain,
driver="BayesLeastSquare",
name="Ellipsometry reconstruction example",
study_id=study_id,
save_dir=optimization_dir_str,
open_browser=True,
)
# Definition of the objective function including derivatives
def objective(**kwargs):
objective_keys = keys.copy()
objective_keys.update(kwargs)
mueller_matrix, mueller_matrix_derivatives = fem_problem.solve(objective_keys)
observation = study.new_observation()
flat_mueller_matrix = mueller_matrix.flatten()
observation.add(flat_mueller_matrix)
if objective_keys["derivative_order"] > 0:
for parameter in optimization_domain:
if parameter["type"] == "continuous":
p = parameter["name"]
derivative_value = mueller_matrix_derivatives[p].flatten()
observation.add(derivative=p, value=derivative_value)
return observation
# Set study parameters
study.set_parameters(
target_vector=target_vector.tolist(),
uncertainty_vector=uncertainty_vector.tolist(),
max_iter=NUM_ITERATIONS,
)
# Run the minimization
study.set_objective(objective)
study.run()
# Plot the reconstruction results and compare it to the target
# First reshape the target vector into a 4x4 matrix
target_matrix = target_vector.reshape(len(wavelengths), 4, 4)
uncertainty_matrix = uncertainty_vector.reshape(len(wavelengths), 4, 4)
# Update the keys with the minimum parameters and get the measurement data
study_info = study.info()
min_params = study_info["min_params"]
keys.update(min_params)
print("Generating reconstruction data for comparison")
reconstructed_mueller_matrix, _ = fem_problem.solve(keys)
fig, ax = plt.subplots(4, 4, figsize=(10, 10), sharex=True)
fig.suptitle("Mueller matrix entries")
for i in range(4):
for j in range(4):
# Set labels
if i == 0 and j == 0:
target_label = dict(label="Target")
reconstructed_label = dict(label="Reconstructed")
else:
target_label = dict()
reconstructed_label = dict()
# Plot data
ax[i, j].plot(wavelengths, target_matrix[:, i, j], **target_label)
ax[i, j].plot(
wavelengths,
reconstructed_mueller_matrix[:, i, j],
**reconstructed_label,
)
ax[i, j].set_title(f"M{i + 1}{j + 1}")
if i == 3:
ax[i, j].set_xlabel("Wavelength (nm)")
plt.figlegend(loc="center", bbox_to_anchor=(0.77, 0.97))
plt.tight_layout()
plt.savefig(optimization_dir / "reconstruction.pdf", bbox_inches="tight")
if __name__ == "__main__":
main()
|
To perform the fit we provide to the optimizer a target vector to which we want to fit the model, and optionally an uncertainty vector which contains the measurement uncertainties associated with each component of the target vector.
161 162 163 164 165 166 | # Set study parameters
study.set_parameters(
target_vector=target_vector.tolist(),
uncertainty_vector=uncertainty_vector.tolist(),
max_iter=NUM_ITERATIONS,
)
|
The optimized objective function computes not a single scalar value but a list of values
that are added to an observation. At each iteration, this vector valued observation is
evaluated. Derivatives can be used to speed up the reconstruction process. As such, the
JCMsuite project is set up to also return parameter derivatives. These are added to the
observation at each iteration.
139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 | # Definition of the objective function including derivatives
def objective(**kwargs):
objective_keys = keys.copy()
objective_keys.update(kwargs)
mueller_matrix, mueller_matrix_derivatives = fem_problem.solve(objective_keys)
observation = study.new_observation()
flat_mueller_matrix = mueller_matrix.flatten()
observation.add(flat_mueller_matrix)
if objective_keys["derivative_order"] > 0:
for parameter in optimization_domain:
if parameter["type"] == "continuous":
p = parameter["name"]
derivative_value = mueller_matrix_derivatives[p].flatten()
observation.add(derivative=p, value=derivative_value)
return observation
|
This particular reconstruction can typically be performed in very few iterations despite containing four different parameters, each with a flat prior.

The parameter reconstruction reaches  values close to 1 after only a few iterations.¶
values close to 1 after only a few iterations.¶
After 20 iterations the Mueller matrix values have been sufficiently reconstructed.

After 20 iterations the reconstructed Mueller matrix entries are indistinguishable from the target vector.¶