Core Mode Filtering¶

In the hollow core example of the parent section we have carefully chosen the eigenvalue guess and the number of eigenmodes to only compute the fundamental mode with maximum confinement in the center of the fiber. However, when designing a fiber this “golden guess” is not known beforehand. For example, when changing the guess slightly one may obtain cladding modes (left) or higher order modes (right) instead of the sought fundamental mode:

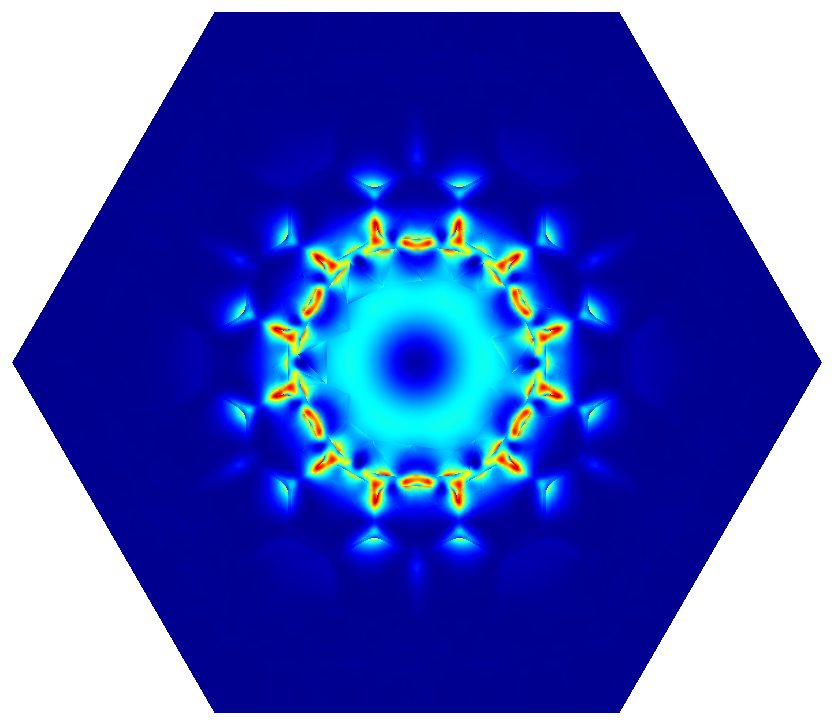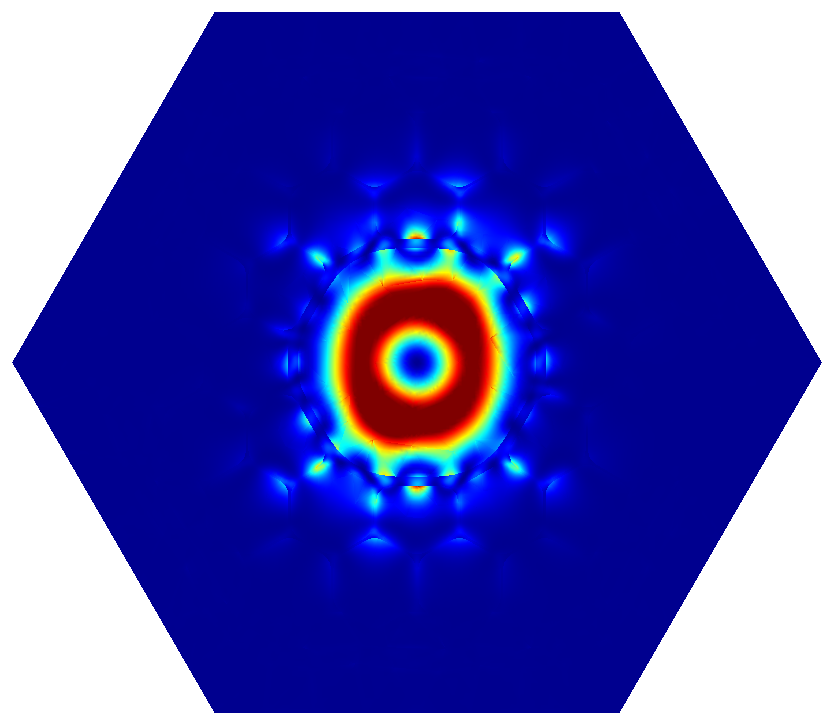To single out the fundamental mode we change the selection criteria in the project definition:

SelectionCriterion {
  Range = [(0.97, 0.0) (0.999, 1e-4)]
  Filter {
    CoreRegion {
      Ellipsoid {
        Center = [0.0 0.0 0.0]
        Diameters = [1.5e-06 1.5e-06 0.0]
      }
    }
    ConfinementFactor = 0.5
  }
}

Instead of a guess we know provide a range, $[n_\mathrm{eff}^\mathrm{(min)} n_\mathrm{eff}^\mathrm{(max)}]$ for the eigenmode search. Without a further restriction this would compute all modes satisfying

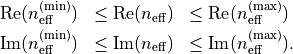
$\begin{eqnarray*} \Re(n_\mathrm{eff}^\mathrm{(min)}) & \leq \Re(n_\mathrm{eff}) & \leq \Re(n_\mathrm{eff}^\mathrm{(max)}) \\ \Im(n_\mathrm{eff}^\mathrm{(min)}) & \leq \Im(n_\mathrm{eff}) & \leq \Im(n_\mathrm{eff}^\mathrm{(max)}). \end{eqnarray*}$

Warning

Choosing a wide range may result in the computation of a large number of modes. You can use the range criteria together with near NearGuess section. Then, only the desired number of modes within the range closest to the guess are computed.

In our example the range is chosen sufficiently small. However, there are still several higher order and cladding modes within this range. To get the fundamental mode only, we specify the core confinement factor within the of the fiber:

Within the CoreRegion section we define the core of the fiber as a circle around zero with diameter 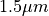$1.5 \mu m$ . In general the core can be described by an union of ellipses, boxes and by a restriction to certain domain ids as constructed in the geometry description in layout.jcm.

With the parameter ConfinementFactor (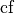 $\mathrm{cf}$ ) we select modes satisfying the following condition:

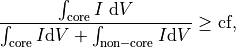
$\begin{eqnarray*} \frac{\int_{\mathrm{core}} I \ \dd V}{\int_{\mathrm{core}} I \dd V +\int_{\mathrm{non-core}} I\dd V} \geq \mathrm{cf}, \end{eqnarray*}$

where 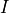$I$ is the field intensity of a mode.