Expression¶
| Type: | string |
|---|---|
| Range: | [] |
| Default: | -/- |
| Appearance: | simple |
| Excludes: | Function, Module |
This parameter is used to define a density tensor field by means of a Python expression within the post-process file.
The syntax is identical to a python based definition of a source field, see for example the section Expression for the definition of an electric field intensity. The expression must set a scalar value defining the density.
As a practical example we want to integrate the electric field energy density 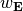 of time-harmonic electric field intensity
of time-harmonic electric field intensity 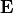 :
:

This density field has two field parameters, namely the electric field intensity 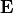 and the complex permittivity tensor
and the complex permittivity tensor  . It may be defined as follows:
. It may be defined as follows:
DensityIntegration {
FieldBagPath = ...
OutputFileName = ...
Python {
IntegralName = "ElectricFieldEnergy"
Expression = "eps0 = 8.85418781762039e-12
D = dot(eps0*eps_rel, E)
D_conj = D.conj()
value = 0.25*dot(D_conj.T, E)"
Parameter {
Name = "E"
FieldValue {
Quantity = ElectricFieldStrength
}
}
Parameter {
Name = "eps_rel"
FieldValue {
Quantity = RelPermittivity
}
}
}
}
In the above, the tag FieldBagPath defines the underlying fieldbag which supplies the meshing for integration. When the underlying fieldbag contains more than one electric field intensity (tagged by ElectricFieldStrength), JCMsolve computes all energies separately.
As a second example, we want to compute overlap integrals of the form
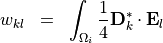
This example involves two fieldbags: One fieldbag delivers the 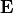 , the other the electric flux density
, the other the electric flux density 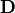 . The two fieldbags may coincide. The JCM input snippet for this example looks like this:
. The two fieldbags may coincide. The JCM input snippet for this example looks like this:
DensityIntegration {
FieldBagPath = ... # path to first fieldbag
OutputFileName = ...
Python {
IntegralName = "OverlapElectricEnergy"
Expression = "D_conj = D.conj()
value = 0.25*dot(D_conj.T, E)"
Parameter {
Name = "D"
FieldValue {
Quantity = ElectricFluxDensity
IntegralIndex = 1
}
}
Parameter {
Name = "E"
FieldValue {
FieldBagPath = ... # path to second fieldbag
Quantity = ElectricFieldStrength
IntegralIndex = 2
}
}
}
}
The Python expression is physically identical to the previous example. However, the field index of the 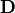 -field parameter runs with the first integral index
-field parameter runs with the first integral index 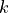 , where as the field index of the
, where as the field index of the 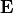 -fields runs with the second integral index
-fields runs with the second integral index 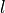 . This way the overlap integrals of all
. This way the overlap integrals of all 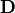 -fields in the first fieldbag with all
-fields in the first fieldbag with all 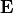 -fields in the second fieldbag are computed.
-fields in the second fieldbag are computed.
As a practical example we want to compute the electromagnetic energy fluxes of a time-harmonic electromagnetic field through domain interfaces. The flux density is the Poynting vector:

This flux density field has two field parameters, namely the electric field intensity 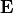 and the magnetic field intensity
and the magnetic field intensity  . The post-process may be defined as follows:
. The post-process may be defined as follows:
DensityIntegration {
FieldBagPath = ...
OutputFileName = ...
InterfaceType = ...
Python {
IntegralName = "ElectromagneticEnergyFlux"
Expression = "value = 0.5*cross(E, H.conj())"
Parameter {
Name = "E"
FieldValue {
Quantity = ElectricFieldStrength
}
}
Parameter {
Name = "H"
FieldValue {
Quantity = MagneticFieldStrength
}
}
}
}
In the above, the tag FieldBagPath defines the underlying fieldbag which supplies the meshing for integration. When the underlying fieldbag contains more than one electromagnetic field, JCMsolve computes all fluxes separately. When choosing InterfaceType=ExteriorDomain the scattered fields  and
and 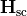 on the interior-exterior domain interfaces are passed.
on the interior-exterior domain interfaces are passed.
As a second example, we want to compute overlap integrals of the form
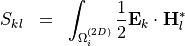
on the cross-section domains of a two-dimensional problem with an infinite  -direction. This requires to set
-direction. This requires to set InterfaceType=CrossSection.
This example involves two fieldbags: One fieldbag delivers the 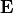 , the other the magnetic field
, the other the magnetic field  . Surely, the two fieldbags may coincide. The JCM input snippet for this example looks like this:
. Surely, the two fieldbags may coincide. The JCM input snippet for this example looks like this:
DensityIntegration {
FieldBagPath = ... # path to first fieldbag
OutputFileName = ...
InterfaceType = CrossSection
Python {
IntegralName = "OverlapCrossSectionEnergyFlux"
Expression = "value = 0.5*cross(E, H.conj())"
Parameter {
Name = "E"
FieldValue {
Quantity = ElectricFieldStrength
}
}
Parameter {
Name = "H"
FieldValue {
FieldBagPath = ... # path to second fieldbag
Quantity = MagneticFieldStrength
}
}
}
}
The Python expression is identical to the previous example. However, the field index of the 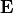 -field parameter runs with the first integral index
-field parameter runs with the first integral index 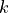 , where as the field index of the
, where as the field index of the  -fields runs with the second integral index
-fields runs with the second integral index 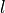 . This way the overlap flux integrals of all
. This way the overlap flux integrals of all 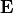 -fields in the first fieldbag with all
-fields in the first fieldbag with all  -fields in the second fieldbag are computed.
-fields in the second fieldbag are computed.