PeriodicPointSource¶

Type:	section
Appearance:	multiple

Defines time-harmonic, Bloch-periodic, dipole sources at positions arranged in a one- or twofold periodic arrangement,

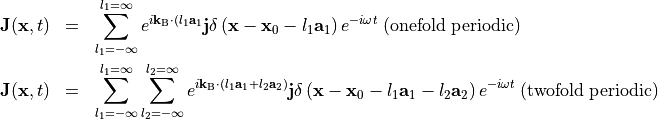
$\begin{eqnarray*} \VField{J}(\pvec{x}, t) & = & \sum_{l_1=-\infty}^{l_1=\infty} e^{i \pvec{k}_\mathrm{B} \cdot (l_1\pvec{a}_1} \VField{j} \delta \left(\pvec{x}-\pvec{x}_0-l_1\pvec{a}_1 \right) e^{-i \omega t}\;\mbox{(onefold\;periodic)} \\ \VField{J}(\pvec{x}, t) & = & \sum_{l_1=-\infty}^{l_1=\infty} \sum_{l_2=-\infty}^{l_2=\infty} e^{i \pvec{k}_\mathrm{B} \cdot (l_1\pvec{a}_1+l_2 \pvec{a}_2)} \VField{j} \delta \left(\pvec{x}-\pvec{x}_0-l_1 \pvec{a}_1 -l_2\pvec{a}_2 \right) e^{-i \omega t}\;\mbox{(twofold\;periodic)} \end{eqnarray*}$

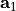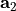Here, $\pvec{a}_1$ , $\pvec{a}_2$ are the lattice vectors, 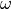$\omega$ is the the angular frequency, 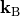$\pvec{k}_\mathrm{B}$ the Bloch vector, 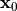$\pvec{x}_0$ is the position of the point source in the unit cell and 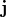$\VField{j}$ is a constant strength vector. The lattice vectors are determined from the specified geometry. Other parameters are set using Omega, K, Position, and Strength, respectively.