BayesOptimization¶

Purpose¶

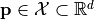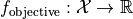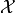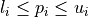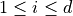The purpose of the driver is to identify a parameter vector $\mathbf{p}\in\mathcal{X}\subset\mathbb{R}^d$ that minimizes the value of an objective function $f_\text{objective}: \mathcal{X} \rightarrow \mathbb{R}$ . The search domain $\mathcal{X}$ is bounded by box constraints $l_i\leq p_i \leq u_i$ for $1\leq i\leq d$ and may be subject to several constraints 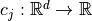$c_j: \mathbb{R}^d \rightarrow \mathbb{R}$ such that 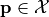$\mathbf{p} \in \mathcal{X}$ only if 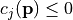$c_j(\mathbf{p}) \leq 0$ (see create_study()).

The driver performs a Gaussian process regression of the objective function. From the regression model it determines parameter values 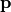$\mathbf{p}$ which lead to a large expected improvement (default behaviour) of the objective function. Compared to other optimization methods, Bayesian optimization requires typically significantly fewer iterations to reach low objective values.

In contrast to other optimization methods, Bayesian optimization allows for mixed domains 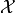$\mathcal{X}$ with discrete and continuous variables. The search for good parameter values includes all possible computation of discrete parameter values. Therfore the number of discrete values should be small (1-3).

Moreover, Bayesian optimization does not require derivatives to perform the optimization. However, if derivatives are available, they can be used to speed up the optimziation.

The regression model allows for a analysis of the objective function based on the samples drawn during the optimization. It is possible to make predictions (predict()), determine the positions and widths of local minima (get_minima()), or compute averages of the objective function for parameter values with a given random distribution (get_statistics()).

Usage Example¶

import sys,os
import numpy as np
import time

sys.path.append(os.path.join(os.getenv('JCMROOT'), 'ThirdPartySupport', 'Python'))
import jcmwave
client = jcmwave.optimizer.client()


# Definition of the search domain
domain = [
    {'name': 'x1', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'x2', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'x3', 'type': 'discrete', 'domain': [-1,0,1]},
    {'name': 'x4', 'type': 'categorial', 'domain': ['cat1','cat2']},
    {'name': 'radius', 'type': 'fixed', 'domain': 2},
]

# Definition of a constraint on the search domain
constraints = [
    {'name': 'circle', 'constraint': 'sqrt(x1^2 + x2^2) - radius'}
]

# Creation of the study object with study_id 'BayesOptimization_example'
study = client.create_study(domain=domain, constraints=constraints,
                            driver="BayesOptimization",
                            name="BayesOptimization example",
                            study_id='BayesOptimization_example')

# Definition of a simple analytic objective function.
# Typically, the objective value is derived from a FEM simulation
# using jcmwave.solve(...)
def objective(**kwargs):
    time.sleep(2) # makes objective expensive
    observation = study.new_observation()
    x1,x2,x3,x4 = kwargs['x1'],kwargs['x2'],kwargs['x3'],kwargs['x4']

    observation.add(10*2
                + (x1**2-10*np.cos(2*np.pi*x1))
                + (x2**2-10*np.cos(2*np.pi*x2))
                + 0.1*x3**2
                + (0 if x4=='cat1' else 1)
            )

    observation.add(derivative='x1', value=2*x1 + 20*np.pi*np.sin(2*np.pi*x1))
    observation.add(derivative='x2', value=2*x2 + 20*np.pi*np.sin(2*np.pi*x2))
    observation.add(derivative='x3', value=2*0.1*x3)

    return observation

# Run the minimization
study.set_objective(objective)
study.run()


info = study.info()
print('Minimum value {:.3f} found for:'.format(info['min_objective']))
for param,value in info['min_params'].items():
    if param == 'x4': print('   {}={}'.format(param,value))
    else: print('   {}={:.3f}'.format(param,value))


#determine local minima of the surrogate model of the objective
minima = study.get_minima()
import pandas as pd
print(pd.DataFrame(minima))

#determine sensitivity of optimum with respect to parameter variations
min_p = info['min_params']
distribution=[
  {'name':'x1', 'distribution':'normal', 'mean':min_p['x1'], 'variance':0.1**2},
  {'name':'x2', 'distribution':'normal', 'mean':min_p['x2'], 'variance':0.1**2},
  {'name':'x3', 'distribution':'fixed', 'value':min_p['x3']},
  {'name':'x4', 'distribution':'fixed', 'value':min_p['x4']},
]
study.set_parameters(distribution=distribution)

statistics = study.get_statistics()

print('Minimum value under parameter variations: {:.3f} +/- {:.3f}'.format(
    statistics['mean'],np.sqrt(statistics['variance'])))

Parameters¶

The following parameters can be set by calling, e.g.

study.set_parameters(example_parameter1 = [1,2,3], example_parameter2 = True)

max_iter (int):	Maximum number of evaluations of the objective function (default: inf)

max_time (int):	Maximum run time in seconds (default: inf)

num_parallel (int):
	Number of parallel observations of the objective function (default: 1)

eps (float):	Stopping criterium. Minimum distance in the parameter space to the currently known minimum (default: 0.0)

min_val (float):
	Stopping criterium. Minimum value of the objective function (default: -inf)

distribution (list):

Definition of random distribution for each parameter in the format of a list. All continuous parameters with unspecified distribution are assumed to be uniformely distributed in the parameter domain. Fixed and discrete parameters are not random parameters. The value of discrete parameters defaults to the first listed value. (default: None)

Example:

[dict(name="param1", distribution="normal", mean=1.0, variance=2.0),
 dict(name="param2", distribution="uniform", domain=[-5,5]),
 dict(name="param3", distribution="gamma", alpha=1.2, beta=0.5),
 dict(name="param4", distribution="fixed", value=7.0),
 dict(name="param5", distribution="beta", alpha=1.5, beta=0.8)]

optimization_step_min (int):
	Minimum number of observations of the objective before the hyperparameters are optimized (default: 2 times number of dimensions). Note: Each derivative observation is counting as an independent observation (default: None)

optimization_step_max (int):
	Maximum number of observations of the objective after which no more hyperparameter optimization is performed. Note: Each derivative observation is counting as an independent observation (default: 300)

optimization_interval (int):
	Maximum number of observations of the objective after which the hyperparameters are optimized. Note: Each derivative observation is counting as an independent observation (default: 20)

compute_suggestion_in_advance (bool):
	If True a suggestion is computed in advance to speed up the sample computation. (default: True)

num_training_samples (int):
	Number of random initial samples before the samples are drawn according to the acquisition function. (default: 0)

parameter_uncertainties (list):

Sometimes, one is interested in minima of the objective function that are preferably insensitive to variations of certain parameters (e.g. if the parameters have large fabrication variances). In this case, one can specify the uncertainties of those parameters, i.e. their standard deviations. The regression model of the objective is averaged over the uncertainty intervals such that very narrow local minima are averaged out whereas broad minima are not effected. Note that the averaging results in additional numerical effort that grows exponentially with the number of uncertain parameters. (default: None)

Example:

[{name="param1", uncertainty=0.1},
 {name="param3", uncertainty=0.2}]

strategy (str):	Sampling strategy of the Bayesian optimization. (default: EI) (options: [‘EI’, ‘LCB’, ‘PoI’])

scaling (float):
	Scaling parameter of the model uncertainty. Default is scaling = 1.0 For scaling >> 1.0 (e.g. scaling=10) the search is more explorative. For scaling << 1.0 (e.g. scaling=0.1) the search becomes more greedy, i.e. any local minimum is intensively exploited (default: 1.0)

vary_scaling (bool):
	If True the scaling parameter is randomly varied between 0.1 and 10 (default: True)

post_converge (bool):
	Converge the minimization using probability of improvement after the min_PoI critereon has been met. (default: False)

min_PoI (float):
	Stopping criterium. Minimum probability of improvement for the last 5 aqcuisitions (default: 0.0)

min_EI (float):	Stopping criterium. Minimum expected improvement for the last 5 aqcuisitions (default: 0.0)

optimization_level (float):
	Steers how often the hyper-parameters are optimized. Small values (e.g. 0.01) lead to more frequent optimizations. Large values (e.g. 1.0) to less frequent optimizations (default: 0.05)

num_samples_hyperparameters (int):
	Number of local searches for optimal hyperparameters. If None, then the number is chosen accordingly to the number of dimensions. (default: None)

num_fantasies (int):
	Number of “fantasy” samples drawn from the Gaussian process in order to average over uncertain function values. This is used for avoiding the position of running samples or to handle noisy inputs. (default: 18)

matern_order (int):
	Order of the used Matern covariance function, i.e. for m=5 the Matern 5/2 function is used. (default: 5)

length_scales (list):
	List of length scales for each parameter on which the objective functions varies. If not set, the length scales are chosen automatically. (default: None)

detect_noise (bool):
	If true, variance due to noise is modelled by two hyperparameter (noise of objective and noise of derivatives). The value of the hyperparameters are chosen to maximize the likelihood of the observations. (default: False)

noise_variance (list):
	List of noise variances for objective observations and derivative observations relative to total variance. If not set, noiseless observations are assumed. Note: If detect_noise is true, the noise variances will be optimized after optimization_step_min observations. (default: None)

warp_input (bool):
	If true, the input function values are transformed (warped) in order to maximize the likelihood of the observations. (default: False)

warping_strengths (list):
	List of lower and upper warping strength. If not set, function values are left unwarped. Note: If warp_input is true, the warping strengths will be optimized after optimization_step_min observations. (default: None)

localize (bool):
	If true, a local search is performed, i.e. samples are not drawn in regions with large uncertainty. (default: False)

horizon (int):	Horizon of previous observations to take into account for driver. (default: all previous observations are taken into account). (default: None)

max_scaling (float):
	Maximum scaling parameter. The scaling parameter is used to enforce a global search after convergence to a local minimum.It is automatically increased when a local convergence has been detected. (default: 10)