L_BFGS_B_Optimization¶

Purpose¶

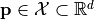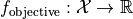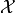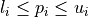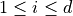The purpose of the driver is to identify a parameter vector $\mathbf{p}\in\mathcal{X}\subset\mathbb{R}^d$ that minimizes the value of an objective function $f_\text{objective}: \mathcal{X} \rightarrow \mathbb{R}$ . The search domain $\mathcal{X}$ is bounded by box constraints $l_i\leq p_i \leq u_i$ for $1\leq i\leq d$ and may be subject to several constraints 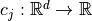$c_j: \mathbb{R}^d \rightarrow \mathbb{R}$ such that 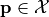$\mathbf{p} \in \mathcal{X}$ only if 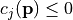$c_j(\mathbf{p}) \leq 0$ (see create_study()).

The driver uses the L-BFGS-B algorithm to perform a gradient-based minimization. We recommend to use the driver if an exact convergence towards a local or global minimum is required. If no derivative information are available, a convergence can be better performed with the derivative-free downhill-simplex minimization.

The implementation of the driver is based on the open source implementation of scipy (see https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html). It is extended to support constraints and a parallel optimization by starting several independent minimizers at different positions.

Usage Example¶

import sys,os
import numpy as np
import time

sys.path.append(os.path.join(os.getenv('JCMROOT'), 'ThirdPartySupport', 'Python'))
import jcmwave
client = jcmwave.optimizer.client()


# Definition of the search domain
domain = [
    {'name': 'x1', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'x2', 'type': 'continuous', 'domain': (-1.5,1.5)},
    {'name': 'radius', 'type': 'fixed', 'domain': 2},
]

# Definition of a constraint on the search domain
constraints = [
    {'name': 'circle', 'constraint': 'sqrt(x1^2 + x2^2) - radius'}
]

# Creation of the study object with study_id 'L_BFGS_B_Optimization_example'
study = client.create_study(domain=domain, constraints=constraints,
                            driver="L_BFGS_B_Optimization",
                            name="L_BFGS_B_Optimization example",
                            study_id='L_BFGS_B_Optimization_example')

# Definition of a simple analytic objective function.
# Typically, the objective value is derived from a FEM simulation
# using jcmwave.solve(...)
def objective(**kwargs):
    time.sleep(2) # makes objective expensive
    observation = study.new_observation()

    x1,x2 = kwargs['x1'], kwargs['x2']
    observation.add(10*2
                + (x1**2-10*np.cos(2*np.pi*x1))
                + (x2**2-10*np.cos(2*np.pi*x2))
            )

    observation.add(derivative='x1', value=2*x1 + 20*np.pi*np.sin(2*np.pi*x1))
    observation.add(derivative='x2', value=2*x2 + 20*np.pi*np.sin(2*np.pi*x2))

    return observation

# Set study parameters
study.set_parameters(max_iter=25, num_parallel=3, num_initial=3, jac=True,
                     initial_samples = [[0.5,0.5],[-0.5,-0.5]])


# Run the minimization
study.set_objective(objective)
study.run()

info = study.info()
print('Minimum value {:.3f} found for:'.format(info['min_objective']))
for param,value in info['min_params'].items():
    if param == 'x4': print('   {}={}'.format(param,value))
    else: print('   {}={:.3f}'.format(param,value))

Parameters¶

The following parameters can be set by calling, e.g.

study.set_parameters(example_parameter1 = [1,2,3], example_parameter2 = True)

max_iter (int):	Maximum number of evaluations of the objective function (default: inf)

max_time (int):	Maximum run time in seconds (default: inf)

num_parallel (int):
	Number of parallel observations of the objective function (default: 1)

eps (float):	Stopping criterium. Minimum distance in the parameter space to the currently known minimum (default: 0.0)

min_val (float):
	Stopping criterium. Minimum value of the objective function (default: -inf)

num_initial (int):
	Number of independent initial optimizers (default: 1)

max_num_minimizers (int):
	If a minimizer has converged, it is restarted at another position. If max_num_minimizers threads have converged, the optimization is stopped (default: inf)

sobol_sequence (bool):
	If true, all initial samples are taken from a Sobol sequence. This typically improves the coverage of the parameter space. (default: True)

jac (bool):	If true, the gradient is used for optimization (default: False)

step_size (float):
	Step size used for numerical approximation of the gradient (default: 1e-06)

f_tol (float):	The iteration stops when 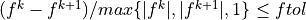$(f^k - f^{k+1})/max\{\|f^k\|,\|f^{k+1}\|,1\} \leq ftol$ . (default: 2.2e-09)