Bayesian Optimization (Part 2)¶ Jupyter Notebook
I this second part of this series we introduce the main concept of Bayesian optimization. Bayesian optimization is based on Gaussian process regression, which was introduced in a previous blog post.
Parameter optimization is a very common task in science and engineering. In photonics it is useful e.g. for the shape optimization of photonic structures or for reconstructing shape parameters from measured data. In the following, we consider the problem of minimizing an objective function (e.g. a loss). Of course, if the target is to maximize an objective, one can equivalently minimize the negative objective.
Definition: Minimization problem
Given a $d$-dimensional parameter space $\mathcal{X} \subset \mathbb{R}^d$ and an objective function $f:\mathcal{X}\rightarrow\mathbb{R}$, find parameter values that minimize the objective. I.e. find $$ \mathbf{x}_{\rm min} = {\rm argmin}_{\mathbf{x}\in\mathcal{X}}f(\mathbf{x})$$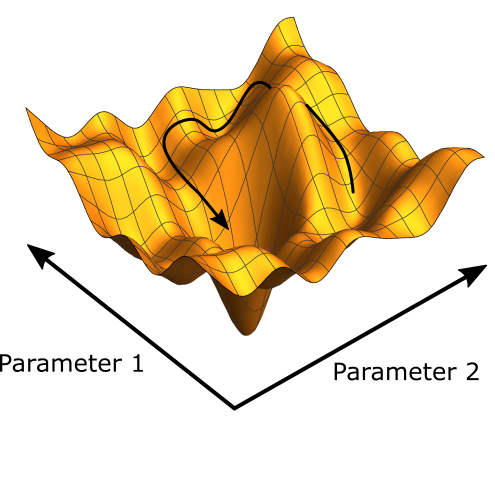
Visualization of a minimization problem for a function depending on two parameters.
Often, one cannot be sure to find the global minimum of an expensive objective function in a reasonable time. Instead, the practical goals of an optimization can be to:
- find the lowest possible $f(\mathbf{x})$ in a given time budget.
- find a value $f(\mathbf{x}) \leq f_{\rm target}$ as fast as possible.
For the sake of concreteness, let us consider a typical optimization task in nanophotonics.
Example: Metasurface¶
Metasurfaces use sub-wavelength structures in order to tailor the optical behavior of a material interface. One application of metasurfaces is to provide an anti-reflective coating for example in order to improve the performance of CCD or CMOS sensors. We consider the example of optimizing a dielectric metasurface in order to suppress the reflectivity for normal incident light between 500 nm and 800 nm wavelength (the visible spectrum from green to red). The parameterization of the design of the periodic surface is depicted in the figure below. The objective is to minimize the average reflectivity $f(\mathbf{s}) = \frac{1}{N}\sum_i^N r(\mathbf{s},\lambda_i)$, where $r(\mathbf{s},\lambda_i)$ is the reflectivity for normal incident light of wavelength $\lambda$ and for a parameter vector $\mathbf{s} = (p,h_{\rm lower},h_{\rm upper},w_{\rm bottom},w_{\rm middle},w_{\rm top})$.
The metasurface consists of a square array of silicon bumps on a silicon substrate. The reflectivity of the structure is minimized with respect to the periodicity of the array ($p$), the heights of the lower and upper part of the bumps ($h_{\rm lower}$ and $h_{\rm upper}$), and the bottom, middle, and top width of the bumps ($w_{\rm bottom}$, $w_{\rm middle}$, and $w_{\rm top}$).
Bayesian Optimization¶
We can now employ the Gaussian process regression (GPR) introduced in the previous blog post to perform an efficient global optimization. The GPR provides for every point $x\in\mathcal{X}$ a prediction in the form of a mean value $\overline{y}(x)$ and a standard deviation $\sigma(x)$. Based on this data, one has to define an acquisition function that determines a score for sampling the expensive black-box function at position $x$. The acquisition function has to make a trade-off between exploration and exploitation. For example, by sampling always at the point of the lowest prediction $\overline{y}(x)$, one can quickly converge into a local minimum (exploitation). However, one converged one would never jump out of the minimum again (exploration). A common choice for an acquisition function, which overcomes this issue, is the expected improvement.
Expected improvement¶
Suppose, we have drawn $t$ samples of the objective function $\mathcal{D}_t=\{(x_1,y_1),\dots,(x_t,y_t)\}$ and the lowest function value found so far is $y_{\rm min}=\min(y_1,\dots,y_t)$. Then, the improvement for a function value of $y$ is defined as $$I(y) = \left\{ \begin{matrix} 0 & \text{for}\;y>y_{\rm min} \\ y_{\rm min} - y &\text{for}\;y<y_{\rm min} \end{matrix}\right.$$
Now, the GPR provides us with a prediction in form of a probability distribution for $y$ such that one can determine the expected improvement $\alpha_{\rm EI} = \mathbb{E}[I(y)]$. Luckily, the expected improvement evaluates to an analytic expression. Suppose for $x^*$ the mean and standard deviation of the Gaussian process regression is given by $\overline{y}=\overline{y}(x^*|\mathcal{D}_t)$ and $\sigma=\sigma(x^*|\mathcal{D}_t)$. Then, $$ \begin{split} \alpha_{\rm EI}(x^*|\mathcal{D}_t) &= \mathbb{E}[I(y)] = \int I(y) P(y) {\rm d}y\\ &= \int_{-\infty}^{y_{\rm min}} \left(y_{\rm min} - y\right)\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(y-\overline{y})^2}{\sigma^2}\right) {\rm d}y\\ &= \frac{\sigma \exp\left(-u^2\right)}{\sqrt{2\pi}} + \frac{1}{2}\left(y_{\rm min}-\overline{y}\right)\left(1 + {\rm erf}(u)\right) \end{split} $$ with $ u = \frac{y_{\rm min}-\overline{y}}{\sqrt{2}\sigma}$
The Bayesian optimization algorithm consists of repeating the following steps:
- Find the maximum of an acquisition function $x_t = {\rm argmax}_x \alpha_{\rm EI}(x|\mathcal{D}_{t-1})$.
- Compute the objective function value $y_t = f(x_t)$ and possibly also the gradient $g_t = \nabla f(x_t)$.
- Update the GPR for the new set of samples $\mathcal{D}_{t} = \mathcal{D}_{t-1} \cup \{(x_t,y_t,g_t)\}$.
The following animation examples show how Bayesian optimization works for a one dimensional objective function. The function is minimized the first time without and the second time with using derivative information.
%matplotlib notebook
from utils import BO_visualization
BO_visualization(use_derivative=False).show()
%matplotlib notebook
from utils import BO_visualization
BO_visualization(use_derivative=True).show()
Real-world examples from nanophotonics¶
In collaboration with the Karlsruhe Institute of Technology (KIT) and the Physikalisch-Technische Bundesanstalt (PTB) we have conducted a benchmark for several typical optimization problems occurring in nanophotonics:
Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction. ACS Photonics, 6(11), 2726-2733 (2019). (arXiv link)
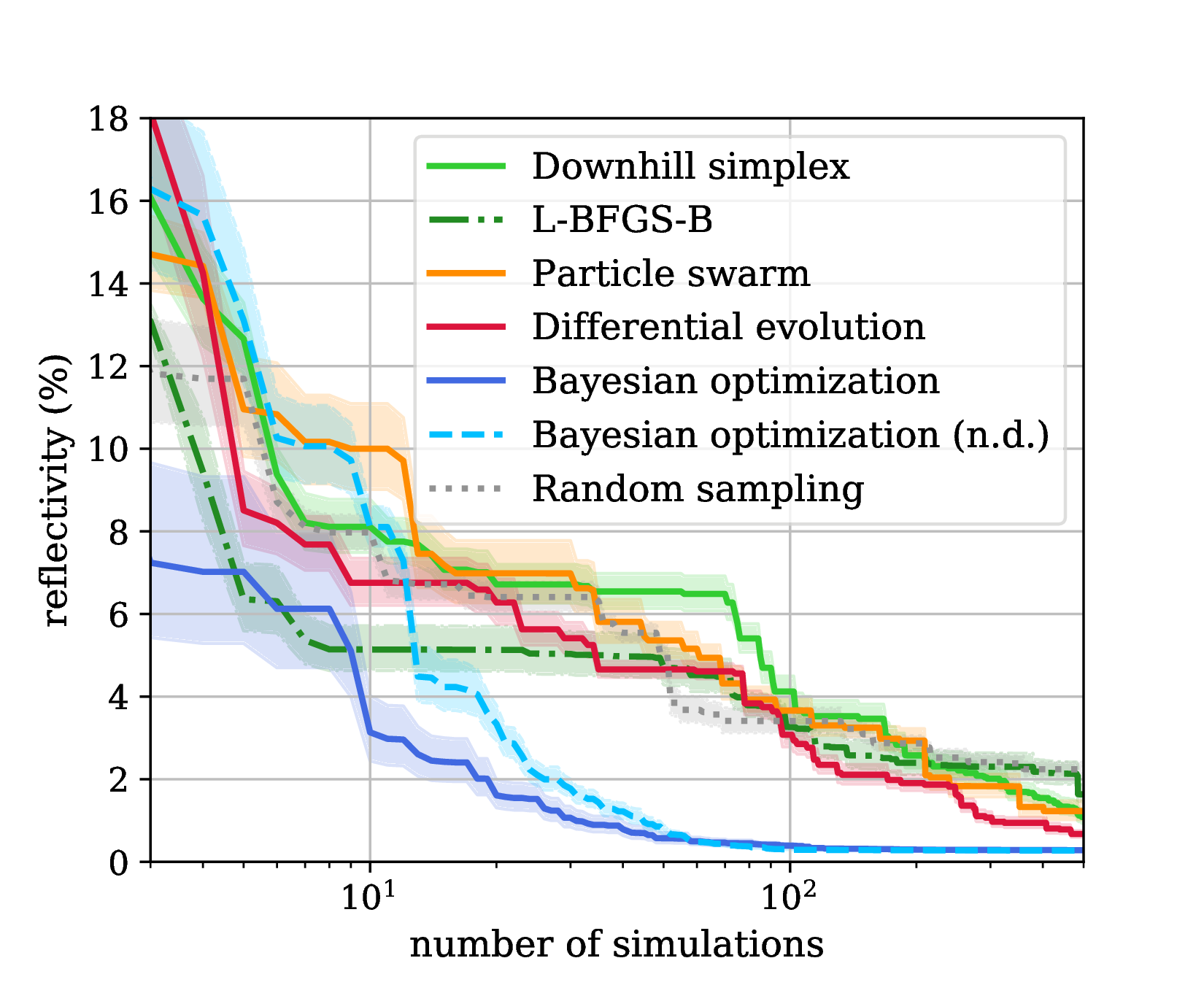
We found that Bayesian optimization is more efficient by about one order of magnitude. The following benchmark from this work considers the optimization of the metasurface introduced above. The benchmark was run on a 6-core Intel Xeon @ 3.2 GHz with 4 parallel evaluations of objective.
Remark on global convergence¶
Bayesian optimization can be very efficient because of the ability of the underlying GPR to build a reliable global model of the objective function based on the previous observations. In order to do this, objective functions must be sufficiently smooth. For example, sharp resonance peaks would lead to extremely short length scales that prevent an interpolation between known data points and an efficient optimization of the objective function.
In the previous blog post, we have seen, that the differentiability of the kernel $k(x,x')$ for $x\rightarrow x'$ and the differentiability of the mean function $\overline{y}(x|\mathcal{D})$ and random functions drawn from the Gaussian process are closely related. It turns out that there is also a strong connection between the differentiability of the Matérn kernel $k_\nu(x,x')$ and the class of objective functions that can be minimized with Bayesian optimization.
As a consequence, using the Matérn kernel $k_\nu(x,x')$ for $\nu=5/2$ the algorithm converges efficiently if the objective function is $\lfloor\nu\rfloor = 2$ times differentiable. However, this result does not imply, that Bayesian optimization necessarily fails if this smoothness properties are not fulfilled.
The smoothness of a function $f$ drawn from a Gaussian process is $1/2$ times smaller than the smoothness of the kernel. Hence, using the Matérn kernel $k_\nu(x,x')$ for $\nu=5/2$, the algorithm converges if the objective function is one time differentiable. Also in this case the result does no imply that Bayesian optimization fails for functions that are not differentiable. Indeed, it is still an open question whether BO even converges for all continuous functions.
Conclusion¶
Bayesian optimization is a highly efficient method for the optimization of expensive black-box functions. Applied to the shape optimization of photonic structures, the computations times can be often reduced by one order of magnitude. From our experience, the shorter optimization times can drastically speed-up the research process as a multitude of different parameterized photonic structures can be easily assessed against each other. Therefore, Bayesian optimization is the default optimization method of JCMsuite's Analysis and Optimization Toolkit of JCMsuite.
Additional Resources¶
- Download a free trial version of JCMsuite.
- Tutorial example on Bayesian optimization based on Gaussian process regression.
- Documentation of JCMsuite's Analysis and Optimization Toolkit for Python and Matlab.
- Publication on benchmark of Bayesian optimization against other optimization methods: Schneider, P. I., Garcia Santiago, X., Soltwisch, V., Hammerschmidt, M., Burger, S., & Rockstuhl, C. (2019). Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction. ACS Photonics, 6(11), 2726-2733. (arXiv link)
- A great reference for Gaussian process regression is the website http://www.gaussianprocess.org/.