Blog
Follow us on Bluesky to stay informed about new blog posts: bsky.app/profile/jcmwave.bsky.social
Tuesday, 02 January 2024 12:00
Reciprocity Applied to Dipole Sources (Part 3)
Written by Phillip ManleyAdditional Info
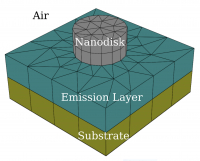
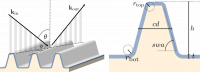
- Abstract This post continues the series on modelling point dipole sources using reciprocity. It shows a concrete example of an ensemble of dipole emitters near a periodic nanostructure, which highlights the computational advantage of exploiting the receprocity theorem.
Wednesday, 27 December 2023 12:00
Reciprocity Applied to Dipole Sources (Part 2)
Written by Phillip ManleyAdditional Info
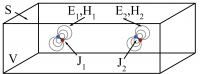
- Abstract This post continues the series on modelling point dipole sources. This post extends the application of the reciprocity theorem to dipoles separated by a large distance. Furthermore, the benefits of the use of the reciprocity principle are discussed.
Tagged under
Friday, 15 December 2023 12:00
Reciprocity Applied to Dipole Sources (Part 1)
Written by Phillip ManleyAdditional Info
- Abstract This post continues the series on modelling point dipole sources by discussing the application of the reciprocity principle to dipoles. In this post, the concept of reciprocity is introduced and applied to the near-fields of dipoles.
Tagged under
Additional Info
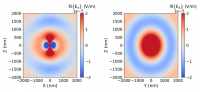
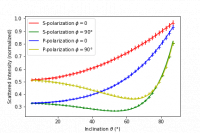
- Abstract This is the second part of a series on dipoles. This post discusses how to evaluate the electromagnetic fields far away from the source. This is useful when modelling the spatial or angular distribution of light on a detector at a large distance form the source.
Tagged under
Additional Info
- Abstract Electric point dipole sources are, along with plane waves, one of the most commonly used sources types in electromagnetic computations. This first post on electric dipoles discusses their near-field properties both from both analytical expressions and numerical simulations in JCMsuite.
Tagged under
Wednesday, 25 August 2021 12:00
Parameter Reconstruction 3: Bayesian Least-Square Reconstruction
Written by Philipp SchneiderAdditional Info
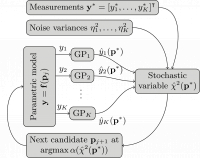
- Abstract This is the third blog posts of a series dedicated to numerical methods for parameter reconstruction. In this postwe try to find the parameters with maximum likelidood based on a set of measurements. In order to do this with a small number of expensive simulations of the measurement process, we use the Bayesian least square method that is part of JCMsuite`s Analysis and Optimization Toolkit. Based on Gaussian process regression, the method learns the dependence of the measurements on the system paramters. This also allows to reconstruct the full posterior probability distribution of the system paramters given the measurement results.
Wednesday, 25 August 2021 12:00
Parameter Reconstruction 2: Variance-Based Sensitivity Analysis
Written by Philipp SchneiderAdditional Info
- Abstract This is the second blog posts of a series dedicated to numerical methods for parameter reconstruction. An important question in the context of parameter reconstruction is how to setup an experimental measurement in order to retrieve enough meaningful information about the system parameters. This post describes the concept of variance-based sensitivity analysis which quantifies the sensitivity of the measurement process to the parameter values.
Wednesday, 25 August 2021 12:00
Parameter Reconstruction 1: Theoretical Introduction
Written by Philipp SchneiderAdditional Info
- Abstract This is the first blog posts of a series dedicated to numerical methods for parameter reconstruction. The overall goal is to determine the value of some system parameters, which are hard to measure directly, based on a set of more easily measurable observables and a numerical model of the measurement process. The first blog contains a brief introduction to the main concepts of parameter reconstruction while the following posts are dedicated to the application of some numerical methods and tools.
Additional Info
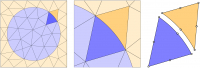
- Abstract This blog post introduces the curvilinear element option for creating curved mesh elements. We assess under which conditions using a curvilinear degree is applicable and quantify the resulting inrease in accuracy.
Additional Info
- Abstract This blog post discusses defining the relative permittivity of materials in JCMsuite. Different methods for taking the frequency dependence of the permittivity into account are presented, including using a model and loading tabulated data from a file.
Friday, 15 January 2021 12:00
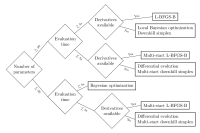
How to choose the right optimization method
Written by Philipp SchneiderAdditional Info
- Abstract This blog post gives some insights in common optimization methods used in computational photonics: L-BFGS-B, the downhill-simplex method, differential evolution, and Bayesian optimization. It tries to give some hints on which method is the best for which optimization problem depending on the number of parameters, the evaluation time of the objective function, and the availability of derivative information.
Tagged under
Friday, 18 December 2020 12:00
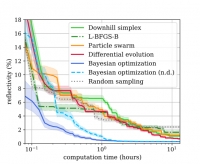
Benchmark of Global Optimization Approaches for Nano-optical Shape Optimization and Parameter Reconstruction
Written by Philipp SchneiderAdditional Info
- Abstract This blog post is based on the publication P.-I. Schneider, et al. Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction.ACS Photonics 6, 2726 (2019). Several global optimization methods for three typical nano-optical optimization problems are benchmarked: particle swarm optimization, differential evolution, and Bayesian optimization as well as multistart versions of downhill simplex optimization and the limited-memory Broydenu2013Fletcheru2013Goldfarbu2013Shanno (L-BFGS) algorithm. In the shown examples, Bayesian optimization, mainly known from machine learning applications, obtains significantly better results in a fraction of the run times of the other optimization methods.
Friday, 11 December 2020 12:00
Gaussian process regression for efficient parameter reconstruction
Written by Philipp SchneiderAdditional Info
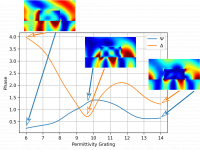
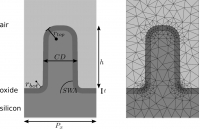
- Abstract This blog post is based on the publication P.-I. Schneider, et al. Using Gaussian process regression for efficient parameter reconstruction.Proc. SPIE 10959, 1095911 (2019). Optical scatterometry is a method to measure the size and shape of periodic micro- or nanostructures on surfaces. For this purpose the geometry parameters of the structures are obtained by reproducing experimental measurement results through numerical simulations. The performance of Bayesian optimization as implemented in JCMsuite`s optimization toolbox is compared to different local minimization algorithms for this numerical optimization problem. Bayesian optimization uses Gaussian-process regression to find promising parameter values. The paper examines how pre-computed simulation results can be used to train the Gaussian process and to accelerate the optimization.
Thursday, 10 December 2020 12:00
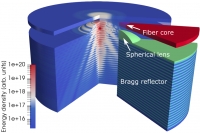
Extraction efficiency of a single-photon emitter into a single-mode fiber
Written by Sven BurgerAdditional Info
- Abstract This blog post is based on the publication P.-I. Schneider, et al. Numerical optimization of the extraction efficiency of a quantum-dot based single-photon emitter into a single-mode fiber. Opt. Express 26, 8479 (2018). The publication introduces a finite-element method for the accurate and efficient simulation of strongly localized light sources, such as quantum dots, embedded in dielectric micro-optical structures. The method is applied in order to optimize the photon extraction efficiency of a single-photon emitter and to study the robustness of the extraction efficiency with respect to fabrication errors and defects.
Tagged under
Additional Info
- Abstract This is the second blog of a series that introduces the concept oy Bayesian optimization (BO). In the first part, we have introduced Gaussian processes as a means to predict the behaviour of the objective function for unkown parameter values. In this second part the BO algorithm is introduced, which uses these predictions to find promising parameter values to sample the expensive objective function. Finally, the performance of BO is compared to other optimization methods showing a great perfomance gain.
Tagged under
Additional Info
- Abstract This is the first blog of a series that introduces the concept oy Bayesian optimization (BO). BO uses a stochastic model of the objective function in order to find promising parameter values. The most commonly applied model is a Guassian process. The first part of the series explains Gaussian processes and Gaussian process regression.
Tagged under