Optical Properties in JCMsuite¶ Jupyter Notebook

When modeling nano-optical systems one stumbling block that comes up again and again is how to describe the optical properties, i.e. the relative permittivity or complex refractive index, of the various physical objects that we want to model. Since JCMsuite solves Maxwell's equations in the frequency domain, it means that only the permittivities for a given frequency are required. Even if a range of frequencies (or alternatively, wavelengths) are required to model the nano-optical system, the permittivities only need to be defined within this range. Since each frequency is modeled independently, experimentally determined values of the permittivity can be directly used as inputs for JCMsuite without the need to fit an analytical model to the data.

Given the flexibility available in defining the permittivity of materials in JCMsuite, the following typical uses cases become easy to handle:

• Using measured values of the permittivity at a single frequency.
• Assuming a constant value for the permittivity valid for all frequencies.
• Using model parameters for one of the permittivity models defined in JCMsuite.
• Combining a constant value with a correction term such as the photoelastic correction.

Furthermore, the JCMsuite scripting interfaces in both Python and Matlab allow the following use cases to be tackled:

• Using measured permittivity values over a range of frequencies.
• Using a model for the permittivity that is not defined within JCMsuite.
• Varying the permittivity over a range of values to study the effect on the model.
• Using the permittivity as an optimization parameter in order to obtain an ideal permittivity for a given application.
• Having complete control over the permittivity by defining a python script that is injected directly into JCMsuite.

The first four points here depend on the scripting interface of JCMsuite to provide appropriate values of the permittivity for a given material. The final use case allows for more advanced descriptions of the permittivity, such as spatial variations within a given material. In the following we limit ourselves to use cases in which the permittivity is homogeneous over a given material.

A Short Note on Permeability¶

The use cases that we will dive into in this post are all for non-magnetic materials, therefore the permeability can safely be set equal to 1 for all cases. Everything presented in the following article that is applied to the permittivity is equally applicable to the permeability if magnetic materials are included in the model.

Overview¶

In the following blog post we will give examples of how to use the scripting interface to vary or optimize the permittivity. Additionally we showcase the dispersion python package which is able to ease the process of loading tables of optical data from file and using them in JCMsuite.

Parameter Scan over Permittivity Values¶

Our first port of call is to use the keyword substitution of the JCMsuite scripting interface to easily run a series of simulations in which we vary the permittivity of a material.

The setup is a 1D dielectric grating, consisting of a periodic array of high dielectric material strips lying on a glass substrate. We simulate the periodic unit cell of the grating, and illuminate it with a plane wave with an incident angle of 30°. We then use the ScatteringMatrix post process of JCMsuite to calculate the ellipsometric $\Psi$ and $\Delta$ coefficients. If you use the download link at the top to retrieve the ZIP file of this Jupyter notebook, all required JCMsuite input files of this example are contained in the folder /sources/parameter_scan.

After creating the three JCMsuite input files needed to define a propagating mode problem (materials.jcm, layout.jcm and project.jcmp) we parameterize the materials.jcm file by creating a parameter from the RelPermittivity. This changes the material file from,

#/sources/parameter_scan/materials.jcm
Material {
  DomainId = 3
  Name = "Grating"
  RelPermeability = 1.0
  RelPermittivity = 9
}

to

#/sources/parameter_scan/materials.jcmt
Material {
  DomainId = 3
  Name = "Grating"
  RelPermeability = 1.0
  RelPermittivity = [%(permittivity_grating)e]
}

and changes the extension to .jcmt. In addition, the project.jcmp.para file is created which lists the parameter we have created,

#/sources/parameter_scan/project.jcmp.para
ProjectParameters {
  permittivity_grating = (9,0)
}

In order to run a parameter scan, a scripting interface needs to be generated. In the following we will use the python interface in JCMsuite, but the same steps could be followed in the Octave/Matlab language to achieve the same results.

Clicking on "analyze" in JCMcontrol opens a menu to specify what kind of scripting task we want to generate. Choosing "Parameter Scan" and jupyter notebook will be generated which can be easily adapted to perform the parameter scan.

In the generated ParameterScan.ipynb we define the values over which we want to vary the permittivity of the strip via,

After using the script to perform the parameter scan, we plot the relationship between the ellipsometric parameters $\Psi$ and $\Delta$ coefficients and the permittivity of the grating. The $\Psi$ and $\Delta$ are defined via the specular amplitude reflection coefficients for s and p polarized light,

Since the wavelength of the computation was held constant at 500 nm, such a permittivity scan represents a thought experiment in which we consider changing the material of the waveguide strip for different materials with a given permittivity at 500 nm. Such a situation might arise when comparing the ellipsometric coefficients of a structure for a set wavelength to measured values.

Another common use case is the computation of a spectrum, in which we vary the frequency (or wavelength) of incident light. If the permittivity of the materials used in the model cannot be assumed to take constant values over the frequency range of interest, then the permittivity must also be set when changing the incident frequency of light. The next example presents one such method of accomplishing this in JCMsuite.

Parameter Scan over the Incident Wavelength¶

In this section we continue looking at the periodic line grating presented in previous section. Instead of varying the permittivity of the strip for a given frequency of light, we instead vary the frequency of light. This, in turn, will cause the permittivity of the grating strip to change. All required JCMsuite input files of this example are contained in the folder /sources/parameter_scan_model.

In order to perform a parameter scan over the frequency of incident light, it is necessary to have a description of the frequency dependence of the permittivity of all the materials needed in the model. In certain cases, it can be a good approximation to assume constant values for the permittivity, e.g. assuming a constant value of 1 for the permittivity of air. However, more often than not, it is precisely the influence of the material dispersion that interests us. In this case we either need a description of the permittivity in a scripting language such as python or Matlab/octave, or we have coefficients for a model that is defined within JCMsuite.

Using a Permittivity Model¶

Our first example will use the Lorentz pole model implemented in JCMsuite to describe the permittivity of the strip. The relative permittivity of a material described by a single Lorentz pole is given via,

Here the constant $\epsilon_{\infty}$ is the high frequency component of the permittivity, $\Delta_{\epsilon}$ defines the strength of the Lorentz pole, $\omega_{p}$ is the pole frequency (also called resonance frequency) and $\gamma$ is the damping factor of the pole. This model can be used to describe materials in which a small number of electronic transitions are important to the permittivity. In the following we use a single Lorentz pole to approximate the permittivity of amorphous silicon (a:Si). To implement this in JCMsuite we again change the material description of the grating strip,

#/sources/parameter_scan_model/materials.jcm
Material {
  DomainId = 3
  Name = "Grating"
  RelPermeability = 1.0
  RelPermittivity = 9
}

which is now replaced by

#/sources/parameter_scan_model/materials.jcmt
Material {
  DomainId = 3
  Name = "Grating"
  RelPermeability = 1.0
  RelPermittivity = {
    Constant = 3.11 # eps_infty
    LorentzPole {
      Damping = 1.46e+15 # gamma
      ResonanceFrequency = 5.97e+15 #omega_p
      Shift = 14.57 # delta_eps
    }
  }
}

We no longer need to parameterize the material of the grating strip, since we are interested in the wavelength dependence of the grating device. The Lorentz pole material model will ensure that the grating strip has the correct permittivity for the wavelength used in the simulation. Instead we now parameterize the wavelength of the incident light, defined in our sources.jcm file,

#/sources/parameter_scan_model/sources.jcmt
SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        3DTo2D = yes
        Lambda0 = %(lambda0)e
        SP = [0 1]
        ThetaPhi = [30, 0]
        Incidence = FromAbove
        PowerFluxScaling = UnitNormal
      }
    }    
  }
}

SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        3DTo2D = yes
        Lambda0 = %(lambda0)e
        SP = [1 0]
        ThetaPhi = [30, 0]
        Incidence = FromAbove
        PowerFluxScaling = UnitNormal
      }
    }    
  }
}

Notice that we have two sources with differing s and p polarizations. Therefore our parameter lamda0 enters the template file twice. The Lorentz pole model in JCMsuite is defined as a function of the angular frequency. When defining a source with the wavelength of light in vacuum instead of the angular frequency, JCMsuite automatically converts the wavelength to an angular frequency to evaluate the Lorentz pole model.

After following the steps outlined in the first section to generate a jupyter notebook based parameter scan, we vary the wavelength of incident light via,

This will scan over the incident wavelength from 300 nm to 1200 nm in steps of 50 nm. After finishing the parameter scan, we can again plot the ellipsometric parameters $\Psi$ and $\Delta$ coefficients, now showing their dependency on the incident wavelength.

The $\Psi$ and $\Delta$ coefficients of the a:Si 1D grating as a function of incident wavelength of light. The a:Si grating strip is modeled via a Lorentz pole. The intensity in the near field of the grating is shown for the cases where the wavelength is 300 nm, 770 nm and 1000 nm.

Using Tabulated Permittivity Values¶

Cases frequently arise in which we wish to directly use experimentally determined permittivity values or in which we wish to use advanced models not available in JCMsuite. In these cases we can perform a parameter scan over the wavelength of light by parameterizing both the source wavelength and the material permittivity. In this example we will load tabulated data for crystalline silicon (c:Si) and use this for the permittivity of the grating strip. All required JCMsuite input files of this example are contained in the folder /sources/parameter_scan_from_file.

We first parameterize Lamdba0 in for both sources in sources.jcmt

#/sources/parameter_scan_from_file/sources.jcmt
SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        3DTo2D = yes
        Lambda0 = %(lambda0)e
        SP = [0 1]
        ThetaPhi = [30, 0]
        Incidence = FromAbove
        PowerFluxScaling = UnitNormal
      }
    }    
  }
}

SourceBag {
  Source {
    ElectricFieldStrength {
      PlaneWave {
        3DTo2D = yes
        Lambda0 = %(lambda0)e
        SP = [1 0]
        ThetaPhi = [30, 0]
        Incidence = FromAbove
        PowerFluxScaling = UnitNormal
      }
    }    
  }
}

Followed by RelPermittivity of the grating strip in materaials.jcmt

#/sources/parameter_scan_from_file/materials.jcmt
Material {
  DomainId = 3
  Name = "Grating"
  RelPermeability = 1.0
  RelPermittivity = [%(permittivity_grating)e]
}

Our project.jcmp.para now has two different parameters:

#/sources/parameter_scan_from_file/project.jcmp.para
ProjectParameters {
    permittivity_grating = (9,0)
    lambda0 = 5e-07
}

We once again follow the steps to generate a jupyter notebook based parameter scan with the wavelength of light as our scan parameter,

Now we need to load the tabulated data and make sure the JCMsuite sets the correct permittivity value for a given wavelength. This process, while simple in principle, can be quite arduous depending on the particular format of the tabulated data. Measured values of the optical data may give the permittivity, the complex refractive index or just the real refractive index. Likewise different communities use different conventions as to the type of spectrum used to measure the data, whether it be a spectrum of wavelength, angular frequency, energy or any number of other conventions. Once the data has been loaded into the scripting language of choice, it must be typically interpolated and then evaluated at the spectral positions used in the JCMsuite simulations.

Dispersion Package¶

In order to make it easier to load and evaluate tabulated optical data, the python package dispersion may be used. This package is available at PyPi: https://pypi.org/project/dispersion/. In this example we wish to load a tabulated data file for c:Si. The file contents begins with,

#SPECTRUMTYPE: energy
#UNIT: ev
#DATATYPE: tabulated nk
0.496	3.442	0.000
0.509	3.443	0.000
0.620	3.449	0.000
0.689	3.458	0.000
0.731	3.464	0.000
...

The data consists of three, tab separated, columns. The first three lines of metadata tell us what the the three columns contain. In this case, the first column gives the energy values in eV at which the data was measured. The second and third columns are the associated n and k values. In order to load this data we make use of the dispersion package,

By plotting the complex refractive index, we can see that the data spans the energy range from under 1 eV to over 6 eV. We can plot the data as a function of the wavelength instead,

We can evaluate the permittivity at a given wavelength,

Note that the wavelength value is automatically converted to energy in eV in order to evaluate the permittivity from the original data set.

We can then integrate this into the keys in the parameter notebook:

After performing the parameter scan over the incident wavelength, we can plot the dependence of the ellipsometric coefficients $\Psi$ and $\Delta$.

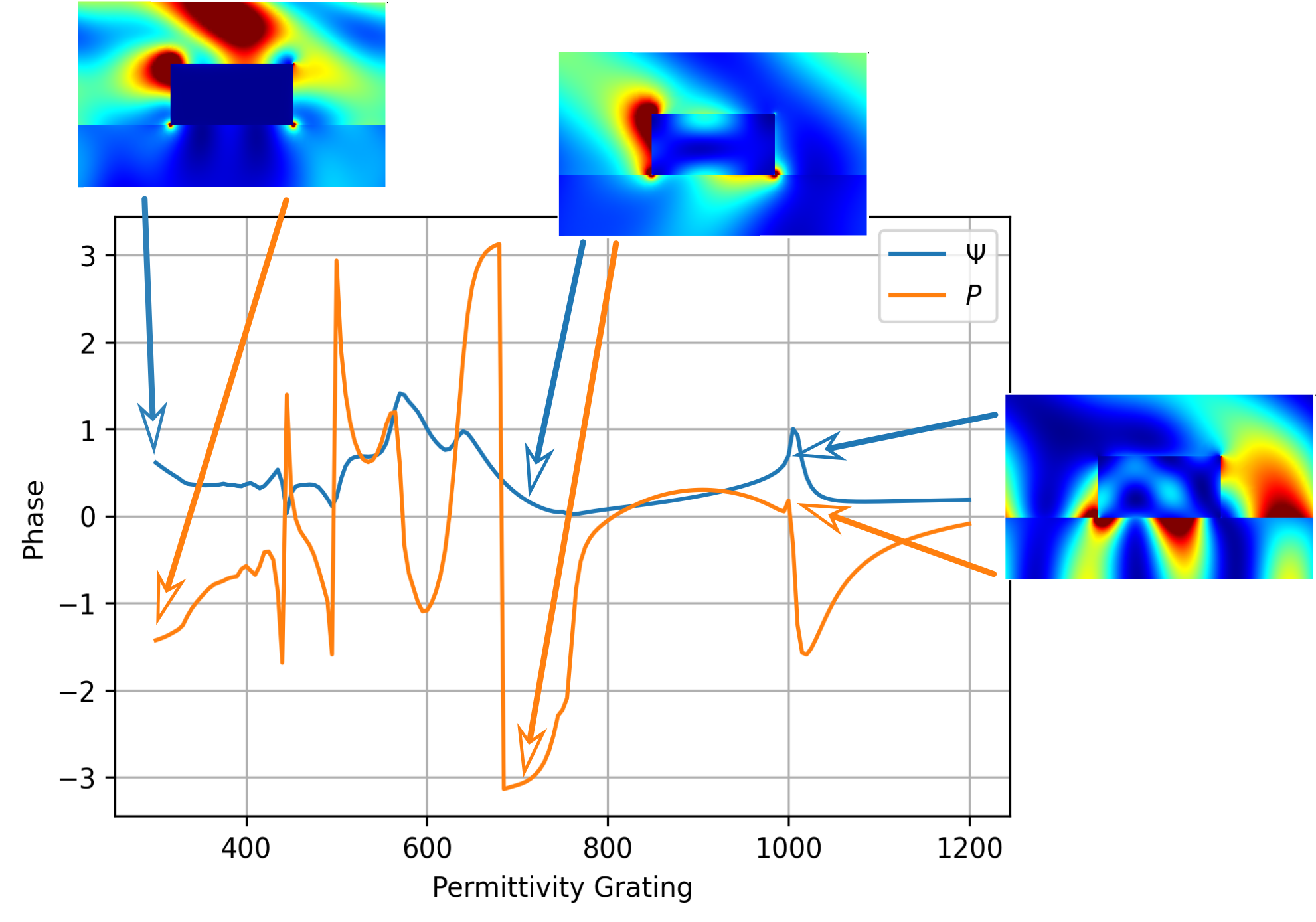The $\Psi$ and $\Delta$ coefficients of the c:Si 1D grating as a function of incident wavelength of light. The permittivity of the c:Si grating strip is given by experimentally determined data loaded from file. The intensity in the near field of the grating is shown for the cases where the wavelength is 300 nm, 700 nm and 1000 nm.

Conclusion¶

In this post we have presented a few methods for defining the relative permittivity of a material in JCMsuite. In particular, we covered the following cases,

• Varying the permittivity directly via a parameter scan
• Varying the permittivity using the Lorentz pole model and scanning the wavelength parameter.
• Varying the permittivity using tabulated experimental data and scanning the wavelength parameter.

More advanced use cases such as more elaborate material models, birefringence, non-linear permittivities, will be left for the content of future posts.

Additional Resources¶

• Download a free trial version of JCMsuite.
• Tutorial example on simulating a 1D line grating in JCMsuite.
• Tutorial example on calculating ellipsometric coefficients for a thin film in JCMsuite.
• Documentation of JCMsuite's scripting interface for Python and Matlab.
• Documentation on defining the relative permittivity in JCMsuite.
• The dispersion python package for loading tabulated optical data.