Reciprocity Applied to Dipole Sources - 3. Advanced Usage¶ Jupyter Notebook
In this post, we will continue the series on modelling point dipole sources using reciprocity. In the previous post, we applied the reciprocity theroem to the far field emission of point dipole sources. We posited that when the number of emission directions in the far field was much smaller than the number of dipole sources we wish to simulate, then applying reciprocity could become beneficial. We will show a concrete example that underlines this principle.
Here we will look at an example of an ensemble of dipole emitter arrays close to a periodic nanostructure. The post is broken down in the following steps:
- Introduction of the periodic nanostructure.
- Numerical simulation of the periodic dipole array using dipole sources.
- Numerical simulation of the periodic dipole array using plane wave sources.
- Comparison of the computational efficiency of the two approaches.
Total Emission of an Ensemble of Periodic Dipole Emitters¶
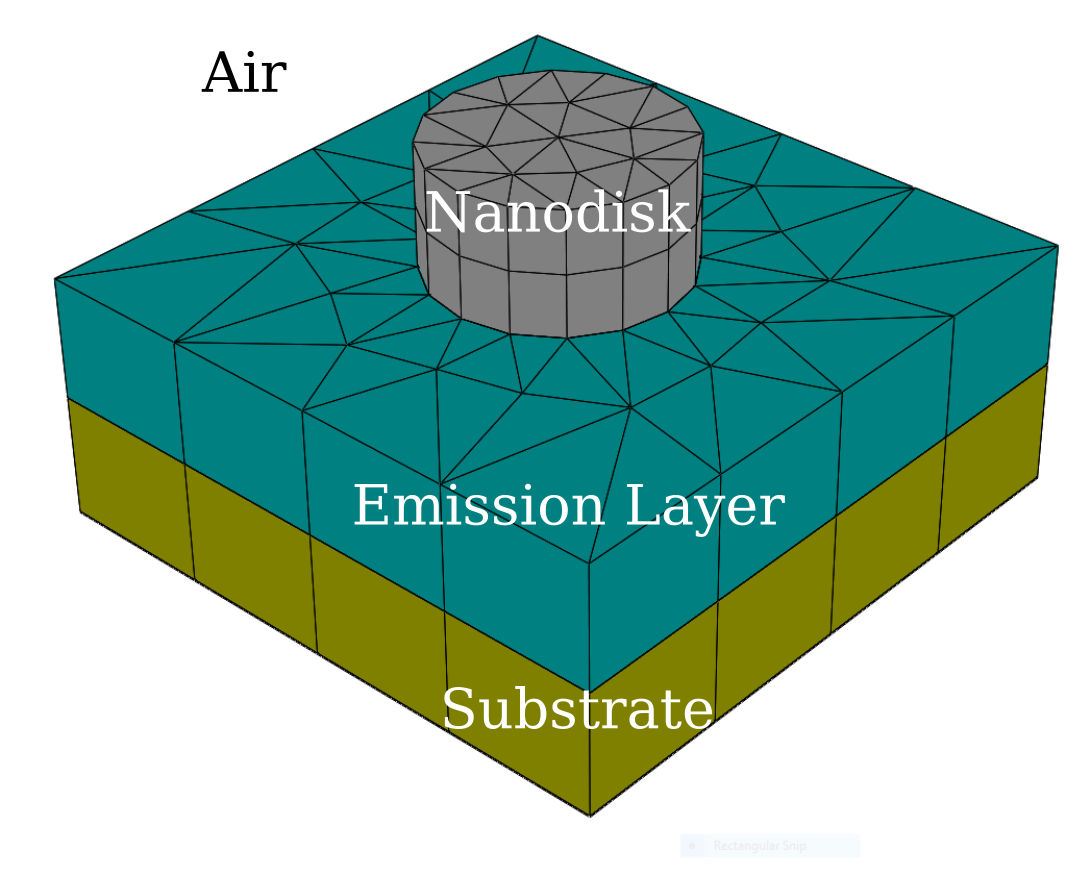
We consider a periodic nanostructure consisting of an array of high dielectric nanodisks sitting on a thin film stacked on a substrate. Figure 1 below shows the periodic unit cell of the structure. The dipole source will be placed inside the thin film, labelled emission layer in fig. 1. Due to the periodic boundary conditions imposed in the $xy$ plane, any dipole source placed in the computational domain will also be repeated periodically. This means that instead of single isolated dipole sources, we are looking at periodic arrays of dipole sources. Such an array of dipole sources will emit into a fixed number of angles in the far field, called diffraction orders, which are dependent on the periodicity of the nanostructure. Importantly, the diffraction order directions are independent of the dipole position inside the computational domain.
Now we consider the case that we wish to know the response for the dipole being at different positions in the unit cell. We might want to average over the volume of the emission layer, since in many applications the position of the dipole source is stochastic. Additionally, the polarization of the emission may also be stochastic, meaning we need to average over the dipole polarization. Each dipole source needs to be simulated three times for $x$, $y$ and $z$ polarizations.
This leads to the stituation of a large number of dipole sources and a small number of emission directions (i.e. diffraction orders) which, as discussed in the previous blog post, can be greatly accelerated by using reciprocity.
Example in JCMsuite¶
Direct approach¶
For the direct approach, a large number of PeriodicPointSource type sources are placed in the sources.jcm file. The number of sources will be $N\times3$ where $N$ is the number of different positions and the factor of three comes from the polarization.
An example of one such source:
SourceBag {
Source {
ElectricCurrentDensity {
PointSource {
Lambda0 = 450e-9
K = [0 0 0]
Position = [-250e-9 -250e-9 20e-9]
Strength = [1 0 0]
}
}
}
}
The wavelength (Lambda0), position and strength parameters should all be familiar from the previous examples of isolated point sources. Here we also have the additional parameter K which describes the phase shift between dipoles when going a unit cell to the neighbouring unit cell. For this example we will leave K equal to the null vector without a loss in generality. Future posts in dipole simulations will cover the meaning of the K parameter and its applications in modelling.
import numpy as np
#dipole positions are in a regular three dimensional grid defined by the following arrays:
x_positions = np.arange(-250, 250, 50)*1e-9
y_positions = np.arange(-250, 250, 50)*1e-9
z_positions = np.arange(20, 100, 20)*1e-9
#that means the total numer of sources needed is: (factor of 3 for polarizations)
n_dipole_sources = x_positions.size*y_positions.size*z_positions.size*3
print(f"# of dipole sources: {n_dipole_sources}")
After solving Maxwell's equations for this large number of sources, we evaluate the FourierTransform and DipoleEmission post processes. These will allow us to easily evaluate the amount of power emitted into the upper and lower half spaces.
import os, sys
sys.path.insert(0,os.path.join(os.getenv('JCMROOT'), 'ThirdPartySupport', 'Python'))
import jcmwave as jcm
source_dir = "sources"
ft_upper = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "dipole_sources",
"project_results", "ft_upper.jcm"))
ft_lower = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "dipole_sources",
"project_results", "ft_lower.jcm"))
de = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "dipole_sources",
"project_results", "de.jcm"))
comp_costs_dipole = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "dipole_sources",
"project_results", "computational_costs.jcm"))
print(f"Time spent assembling problem: \t{comp_costs_dipole['TotalTimeAssembling'][0]/60.:.0f} minutes")
print(f"Time spent solving problem: \t{comp_costs_dipole['TotalTimeSolve'][0]/60.:.0f} minutes")
print(f"Total time for all steps: \t{comp_costs_dipole['TotalTime'][0]/60.:.0f} minutes")
Due to the large number of sources, the assembling step of JCMsuite is much larger than the solving step. We wish to acheive the same results without the overhead of assembling many different sources.
Reciprocal approach¶
As outlined above, the reciprocal approach will involved simulating the same geometry using plane wave sources. In order to simplify the generation of our plane wave sources, we use the BlochFamily option in JCMsuite. This option automatically generates all the propagating diffraction orders for a given periodic until cell and wavelength of light. The syntax for a Bloch family is straightforward,
MultipleSources {
BlochFamily {
Lambda0 = 450e-9
Sigma = [0 0]
Incidence = FromAbove
OutputFileName = "Bloch_family_FromAbove.jcm"
}
Here the parameter Sigma refers to the phase shift between field solutions when going from one until cell to a neighbouring unit cell. This is equivalent to the K parameter of the PeriodicPointDipole source type, except the units are in so called sigma coordinates instead of inverse meters as for the K parameter. For an explanation of sigma coordinates, take a look at the documentation for plane wave sources.
We add two Bloch families, one for the upper and one for the lower half space. Due to the combination of periodicity and wavelength, there are 14 diffraction orders, which each need to be simulated for two linearly independent polarisations, totalling to 28 sources.
bloch_family_from_above = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission",
"plane_wave_sources", "Bloch_family_FromAbove.jcm"))
bloch_family_from_below = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission",
"plane_wave_sources", "Bloch_family_FromBelow.jcm"))
n_pw_sources = bloch_family_from_above['K'].shape[0] + bloch_family_from_below['K'].shape[0]
print(f"# of plane wave sources: \t{n_pw_sources}")
efield = jcm.loadcartesianfields(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "plane_wave_sources",
"project_results", "efield.jcm"))
comp_costs_pw = jcm.loadtable(os.path.join(source_dir, "multiple_periodic_dipoles_emission", "plane_wave_sources",
"project_results", "computational_costs.jcm"))
print(f"Time spent assembling problem: \t{comp_costs_pw['TotalTimeAssembling'][0]:.0f} seconds")
print(f"Time spent solving problem: \t{comp_costs_pw['TotalTimeSolve'][0]:.0f} seconds")
print(f"Total time for all steps: \t{comp_costs_pw['TotalTime'][0]:.0f} seconds")
print(f"Speed up due to reciprocity: \t{comp_costs_dipole['TotalTime'][0]/comp_costs_pw['TotalTime'][0]:.1f} times faster")
Note that due to the reduced number of sources, both the assembling and solve time were reduced, with the largest gains coming from the reduced assembling time. In total a factor of over $64\times$ speedup is acheived by applying reciprocity. After solving Maxwell's equations, we use the ExportField post process to evaluate the field strength at the positions of our our 400 dipole source positions.
Calculate a Fourier Transform via reciprocity¶
In the previous section, we calculated the field strength inside the emission layer due to plane wave sources. To obtain the total emission to the far field, we still need to apply reciprocity. In the following, we calculate the Fourier transform of the outgoing emission into the upper half space for a single dipole position and polarization using reciprocity. We then compare this to the result using direct dipole simulations for each diffraction order in the upper half space.
n_bf_directions = int(bloch_family_from_above['K'].shape[0]/2)
n_pw_polarizations = 2
#Obtain amplitude normalisation factor
computational_domain_area = (500e-9)**2
power_norm = 1./computational_domain_area
amplitude_norm = np.sqrt(power_norm)
dipole_current = np.array([1., 0., 0.])
#Initialise data structure that will become our Fourier transform
fourier_transform = {}
fourier_transform['K'] = np.zeros((n_bf_directions, 3), dtype=np.complex128)
fourier_transform['ElectricFieldStrength'] = np.zeros((n_bf_directions, 3), dtype=np.complex128)
for i_bf in range(n_bf_directions):
fourier_mode_sp = np.zeros((1, 3), dtype=np.complex128)
for i_pw_pol in range(n_pw_polarizations):
pw_index = np.ravel_multi_index((i_bf, i_pw_pol), (n_bf_directions, n_pw_polarizations))
current_k = bloch_family_from_above['K'][pw_index]
efield_at_dp_pos = efield['field'][pw_index][0, 0, 0, :] # first dipole
normalization_factor = 0.25*amplitude_norm
expansion_coefficient = normalization_factor*efield_at_dp_pos.dot(dipole_current).T
pw_amp = bloch_family_from_above['Amplitude'][0][pw_index, :]
fourier_mode_sp += expansion_coefficient*pw_amp*amplitude_norm
fourier_transform['K'][i_bf, :] = -current_k
fourier_transform['ElectricFieldStrength'][i_bf, :] = -fourier_mode_sp
for row in range(fourier_transform['K'].shape[0]):
current_k_reciprocal = fourier_transform['K'][row, :]
for row2 in range(ft_upper['K'].shape[0]):
current_k = ft_upper['K'][row2, :]
if np.linalg.norm(current_k_reciprocal-current_k)< 1e-3:
e_recip = fourier_transform['ElectricFieldStrength'][row, :]
e_direct = ft_upper['ElectricFieldStrength'][0][row2, :]
n1 = ft_upper['N1'][row2]
n2 = ft_upper['N2'][row2]
relative_error = np.linalg.norm(np.abs(e_recip-e_direct))/np.linalg.norm(np.abs(e_direct))
print(f"relative error for ({n1},{n2}) diffraction order: \t{relative_error:.8e}")
Calculate Total Emission for an Ensemble of Dipoles¶
The final step in this tutorial is to determine the total emission of the array of incoherent dipoles. In order to iterate over all the sources and polarizations we need to perform the following iterations (here in pseudocode):
iterate dipole position
iterate dipole polarization
iterate plane wave incident half space
iterate plane wave incident angle
iterate plane wave incident polarization
apply reciprocity
superimpose polarizations
determine contribution to total emission
The following script presents an implementation of the above algorithm,
from scipy import constants
n_pw_polarizations = 2
computational_domain_area = (500e-9)**2
power_norm = 1./computational_domain_area
amplitude_norm = np.sqrt(power_norm)
permittivity_upper = 1.
permittivity_lower = 2.
X, Y, Z = np.meshgrid(x_positions, y_positions, z_positions)
total_dipole_emission = 0.
for ix in range(x_positions.size):
for iy in range(y_positions.size):
for iz in range(z_positions.size):
for idp_pol in range(3):
if idp_pol == 0:
dipole_current = np.array([1., 0., 0.])
elif idp_pol == 1:
dipole_current = np.array([0., 1., 0.])
elif idp_pol == 2:
dipole_current = np.array([0., 0., 1.])
for i_hs, inc_direction in enumerate(['FromAbove', 'FromBelow']):
if i_hs == 0:
bloch_family = bloch_family_from_above
permittivity = permittivity_upper
elif i_hs == 1:
bloch_family = bloch_family_from_below
permittivity = permittivity_lower
n_bf_directions = int(bloch_family['K'].shape[0]/2)
fourier_transform = {}
fourier_transform['K'] = np.zeros((n_bf_directions, 3), dtype=np.complex128)
fourier_transform['ElectricFieldStrength'] = np.zeros((n_bf_directions, 3), dtype=np.complex128)
for i_bf in range(n_bf_directions):
fourier_mode_sp = np.zeros((1, 3), dtype=np.complex128)
for i_pw_pol in range(n_pw_polarizations):
pw_index = np.ravel_multi_index((i_bf, i_pw_pol), (n_bf_directions, n_pw_polarizations))
current_k = bloch_family['K'][pw_index]
if inc_direction == 'FromAbove':
total_pw_index = pw_index
elif inc_direction == 'FromBelow':
total_pw_index = pw_index + bloch_family_from_above['K'].shape[0]
efield_at_dp_pos = efield['field'][total_pw_index][ix, iy, iz, :]
normalization_factor = 0.25*amplitude_norm
expansion_coefficient = normalization_factor*efield_at_dp_pos.dot(dipole_current).T
pw_amp = bloch_family['Amplitude'][0][pw_index, :]
fourier_mode_sp += expansion_coefficient*pw_amp*amplitude_norm
fourier_transform['K'][i_bf, :] = -current_k
fourier_transform['ElectricFieldStrength'][i_bf, :] = -fourier_mode_sp
prefactor = 0.5*np.sqrt(permittivity*constants.epsilon_0/constants.mu_0)
angle_factor = np.abs(np.real(current_k[2])/np.real(np.linalg.norm(current_k)))
emission = prefactor*angle_factor*np.linalg.norm(np.abs(fourier_mode_sp))**2/power_norm
total_dipole_emission += emission
total_dipole_emission /= n_dipole_sources
print(f"Total emission from ensemble of dipoles via reciprocity: {total_dipole_emission:.8e} W")
total_dipole_emission2 = 0.
for ii in range(len(de['DipoleEmission'])):
total_dipole_emission2 += de['DipoleEmission'][ii]
total_dipole_emission2 /= n_dipole_sources
print(f"Total emission from ensemble of dipoles via direct simulations: {total_dipole_emission2:.8e} W")
print(f"Relative error on ensemble dipole emission: {np.abs(total_dipole_emission-total_dipole_emission2)/total_dipole_emission:.3e}")
The agreement between the direct and reciprocal methods is excellent and comes with the advantage of a $64\times$ speed up in computation time.
Conclusion¶
The reciprocity theorem is a powerful tool for simplifying electromagnetic simulations. In particular, when the number of sources needed can be reduced by reformulating the probelem in terms of reciprocal sources. In this post, we have looked at the following examples of using reciprocity:
- Arrays of periodic dipoles at different positions in a periodic nanostructure were simulated using 1200 dipole sources.
- The same physical model was simulated using 24 plane wave sources.
- The Fourier Transform resulting from a single dipole position was shown to be equivalent between the direct and reciprocal methods.
- The total dipole emission when averaging over all dipole array positions was also shown to be equivalent when comparing the two methods.
- By applying reciprocity a $64\times$ speedup in computation time was achieved.
Additional Resources¶
- Download a free trial version of JCMsuite.
- Documentation for periodic dipole sources in JCMsuite can be found here.
- Documentation for Bloch families in JCMsuite can be found here
- Documentation for the export field post process in JCMsuite can be found here
- Documentation for the Fourier transform post process in JCMsuite can be found here
- Documentation for the dipole emission post process in JCMsuite can be found here
