Displaying items by tag: optimization and parameter retrieval methods
Published in 2024
Published in 2023
Published in 2023
Published in 2022
Published in 2022
Published in 2021
Published in 2018
Published in 2014
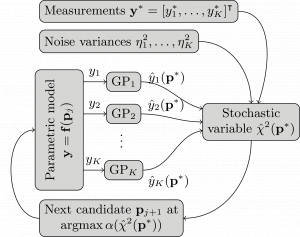
This is the third blog posts of a series dedicated to numerical methods for parameter reconstruction. In this postwe try to find the parameters with maximum likelidood based on a set of measurements. In order to do this with a small number of expensive simulations of the measurement process, we use the Bayesian least square method that is part of JCMsuite`s Analysis and Optimization Toolkit. Based on Gaussian process regression, the method learns the dependence of the measurements on the system paramters. This also allows to reconstruct the full posterior probability distribution of the system paramters given the measurement results.
Published in Blog
Tagged under
This is the second blog posts of a series dedicated to numerical methods for parameter reconstruction. An important question in the context of parameter reconstruction is how to setup an experimental measurement in order to retrieve enough meaningful information about the system parameters. This post describes the concept of variance-based sensitivity analysis which quantifies the sensitivity of the measurement process to the parameter values.
Published in Blog
Tagged under
This is the first blog posts of a series dedicated to numerical methods for parameter reconstruction. The overall goal is to determine the value of some system parameters, which are hard to measure directly, based on a set of more easily measurable observables and a numerical model of the measurement process. The first blog contains a brief introduction to the main concepts of parameter reconstruction while the following posts are dedicated to the application of some numerical methods and tools.
Published in Blog
Tagged under
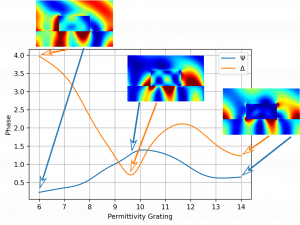
This blog post discusses defining the relative permittivity of materials in JCMsuite. Different methods for taking the frequency dependence of the permittivity into account are presented, including using a model and loading tabulated data from a file.
Published in Blog
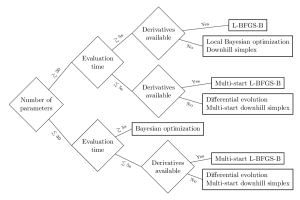
This blog post gives some insights in common optimization methods used in computational photonics: L-BFGS-B, the downhill-simplex method, differential evolution, and Bayesian optimization. It tries to give some hints on which method is the best for which optimization problem depending on the number of parameters, the evaluation time of the objective function, and the availability of derivative information.
Published in Blog
Tagged under
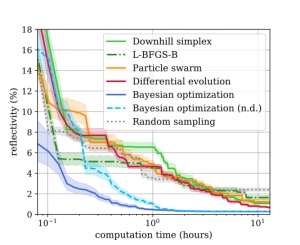
This blog post is based on the publication P.-I. Schneider, et al. Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction.ACS Photonics 6, 2726 (2019). Several global optimization methods for three typical nano-optical optimization problems are benchmarked: particle swarm optimization, differential evolution, and Bayesian optimization as well as multistart versions of downhill simplex optimization and the limited-memory Broydenu2013Fletcheru2013Goldfarbu2013Shanno (L-BFGS) algorithm. In the shown examples, Bayesian optimization, mainly known from machine learning applications, obtains significantly better results in a fraction of the run times of the other optimization methods.
Published in Blog
Tagged under
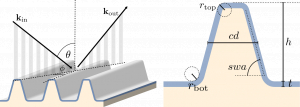
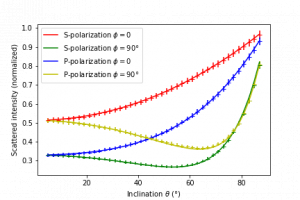
This blog post is based on the publication P.-I. Schneider, et al. Using Gaussian process regression for efficient parameter reconstruction.Proc. SPIE 10959, 1095911 (2019). Optical scatterometry is a method to measure the size and shape of periodic micro- or nanostructures on surfaces. For this purpose the geometry parameters of the structures are obtained by reproducing experimental measurement results through numerical simulations. The performance of Bayesian optimization as implemented in JCMsuite`s optimization toolbox is compared to different local minimization algorithms for this numerical optimization problem. Bayesian optimization uses Gaussian-process regression to find promising parameter values. The paper examines how pre-computed simulation results can be used to train the Gaussian process and to accelerate the optimization.
Published in Blog
Tagged under
This is the second blog of a series that introduces the concept oy Bayesian optimization (BO). In the first part, we have introduced Gaussian processes as a means to predict the behaviour of the objective function for unkown parameter values. In this second part the BO algorithm is introduced, which uses these predictions to find promising parameter values to sample the expensive objective function. Finally, the performance of BO is compared to other optimization methods showing a great perfomance gain.
Published in Blog
Tagged under